Plantilla:Perímetros y áreas
De Wikipedia
| Revisión de 18:52 15 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:14 15 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 67: | Línea 67: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rectángulo; en la segunda podrás calcular el área y el perímetro del rectángulo. | |descripcion=En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rectángulo; en la segunda podrás calcular el área y el perímetro del rectángulo. | ||
| - | |enlace=[https://ggbm.at/v3v8CeDM Área y perímetro del rectángulo ] | + | |enlace=[https://ggbm.at/v3v8CeDM Área y perímetro del rectángulo] |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 157: | Línea 157: | ||
| :Un rombo es un paralelogramo con los cuatro lados iguales.{{p}} | :Un rombo es un paralelogramo con los cuatro lados iguales.{{p}} | ||
| }} {{p}} | }} {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Rombo''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rombo; en la segunda podrás calcular el área y el perímetro del rombo. |
| - | |enunciado='''Actividad 1:''' Deducción del área del rombo. | + | |enlace=[https://ggbm.at/XXSVrP87 Área y perímetro del rombo ] |
| + | }} | ||
| {{p}} | {{p}} | ||
| - | |actividad=Modifica el polígono arrastrando los puntos verdes | ||
| - | *¿Qué relación hay entre el área del rombo y la del rectángulo circunscrito? | ||
| - | *¿Cuál será la formula que permita calcular el área de un rombo a partir de sus diagonales? ¿Por qué? | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/area_rombo.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/area_rombo.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | |||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' La diagonal mayor de un rombo mide 5m, y la menor es la mitad. Calcula el área y el perímetro del rombo. | ||
| - | |actividad= | ||
| - | Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geometria/geoweb/area3_2.html | ||
| - | width=430 | ||
| - | height=330 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>'''Cálculo del área y del perímetro del rombo'''</center> | ||
| - | <center>(Mueve los vértices para modificar la medida de los lados)</center> | ||
| - | <center>[http://maralboran.org/web_ma/geometria/geoweb/area3_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 3:''' | ||
| - | Calcula el área de un cuadrado de 4 m. de diagonal. | ||
| - | :a) Utilizando el teorema de Pitágoras para determinar el lado. | ||
| - | :b) Utilizando la fórmula del área del rombo. | ||
| {{p}} | {{p}} | ||
| - | |actividad= | ||
| - | El cuadrado es un rombo que tiene las diagonales iguales. | ||
| - | Para calcular el área del cuadrado puedes utilizar también la expresión del área del rombo. | ||
| - | Comprueba en la figura que estas expresiones dan el mismo valor. | ||
| - | <center><iframe> | + | {{wolfram desplegable|titulo=El rombo|contenido= |
| - | url=http://maralboran.org/web_ma/geometria/geoweb/area3_3.html | + | |
| - | width=430 | + | |
| - | height=330 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>'''El cuadrado es un rombo con los 4 lados iguales'''</center> | + | |
| - | <center>(Mueve el vértice B para modificar la medida del lado)</center> | + | |
| - | <center>[http://maralboran.org/web_ma/geometria/geoweb/area3_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| {{wolfram | {{wolfram | ||
| - | |titulo=Actividad: ''Rombo'' | + | |titulo=Actividad: ''El rombo'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| Línea 232: | Línea 184: | ||
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| - | + | }} | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 20:14 15 nov 2016
Tabla de contenidos |
Cuadrado

|
|
|
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del cuadrado; en la segunda podrás calcular el área y el perímetro del cuadrado.
|
Actividad: El cuadrado
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
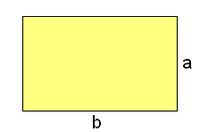
Rectángulo
|
|
|
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rectángulo; en la segunda podrás calcular el área y el perímetro del rectángulo.
|
Actividad: El rectángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Paralelogramo

|
|
|
En esta escena podrás deducir la fórmula del área del paralelogramo y practicar con ella.
|
Actividad: El paralelogramo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
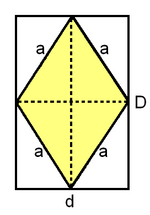
Rombo
|
|
|
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rombo; en la segunda podrás calcular el área y el perímetro del rombo.
|
Actividad: El rombo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Triángulo
|
|
|
Actividad interactiva: Triángulo Actividad 1: Deducción del área del triángulo. Actividad: Desliza el punto verde o utiliza los botones, observa lo que ocurre y razona:
Vuelve a la posición inicial y modifica el triángulo arrastrando cualquiera de sus vértices. Vuelve a deslizar los puntos verdes.
Vuelve a la posición inicial y modifica el triángulo arrastrando cualquiera de sus vértices. Vuelve a deslizar el punto verde.
Actividad 2: La base de un triángulo isósceles mide 5 cm. y los lados iguales miden 3,7 cm. Halla su área y su perímetro.
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: El cuadrado es un rombo con los 4 lados iguales
(Mueve los vértices del triángulo para variar la medida de los lados)
|
Fórmula de Herón
La superficie de un triángulo de lados a, b, c viene dada por:
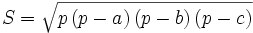
donde 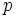 es el semiperímetro:
es el semiperímetro: 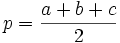 .
.
Nota: Esta demostración excede el nivel de este curso.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados a, b, c cuyos ángulos opuestos a cada uno de esos lados son A, B, C. Entonces tenemos que:
por el Teorema del coseno:
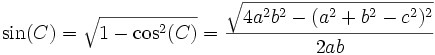 .
.
La altura de un triángulo de base a tiene una longitud bsin(C), por tanto siguiendo con la demostración
|
Actividad: Triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
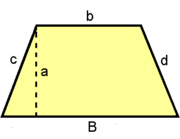
Trapecio
|
|
|
|
Actividad interactiva: Trapecio
1. Deducción de la fórmula del área de un trapecio.
Actividad: Para ello, mueve el punto rojo hacia la izquierda. Obtendrás un duplicado del trapecio en color azul, que junto con el trapecio amarillo inicial, forman un paralelogramo de base 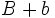 y altura y altura  . .
El área del paralelogramo es: 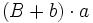 de donde, dividiendo por 2, obtenemos el área del trapecio: 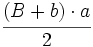 Deducción de la fórmula del área del trapecio
(Mueve el punto rojo)
2. Halla el área y el perímetro de un trapecio de base mayor 5 cm., base menor 1,5 cm. y altura 2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y del perímetro de un trapecio
(Mueve los vértices del trapecio para variar la medida de los lados)
3. Halla el área y el perímetro de un trapecio rectángulo de base mayor 4,5 cm., base menor 3 cm. y altura 1,2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y del perímetro de un trapecio rectángulo
4. Halla el área y el perímetro de un trapecio isósceles de base mayor 4 cm., base menor 2,4 cm. y lado L=2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y el perímetro de un trapecio isósceles
(Mueve los vértices del trapecio para variar la medida de los lados) |
|
Actividad: Trapecio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
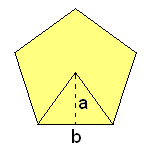
Polígonos regulares
|
|
|
|
Actividad interactiva: Polígono regulares Actividad 1: Deducción del área de un polígono regular. Actividad: Desliza el punto verde y observa
Actividad 2:
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Calculo del área y del perímetro de un polígono regular.
(Mueve los puntos azules para variar el número de lados y la medida de los mismos)
Pero, para determinar el área, necesitamos conocer, además del lado, la apotema. Si conocemos uno de ellos y el radio, podemos hallar el otro por el Teorema de Pitágoras, como se observa en la siguiente escena: Calculo de la apotema, lado o radio de un polígono regular.
(Mueve los puntos azules para variar el número de lados y la medida de los mismos)
Actividad 3: Cálculo del área y del perímetro de un polígono regular. Actividad: En esta escena puedes comprobar el área, perímetro, apotema y lado de un polígono regular haciendo variar al radio. Desliza el punto verde para modificar el número de lados.
|
|
Actividad: Polígonos regulares
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
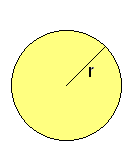
Círculo
|
|
|
|
Actividad interactiva: Círculo Actividad 1: Comprobación de la fórmula de la longitud de la circunferencia. Actividad 2: Aproximación a la fórmula del área del círculo.
Actividad 3: En un círculo de radio 1,71 cm, halla su área y la longitud de su circunferencia.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área y del perímetro de un círculo.
|
|
Actividad: Círculo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
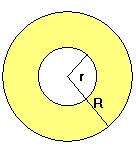
Corona circular
|
|
|
|
Actividad interactiva: Corona circular
1. Halla el área de una corona circular cuyos círculos tienen de radio 2 cm y 1,37 cm, respectivamente.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de una corona circular
(Mueve el punto azul para modificar el radio pequeño)
|
|
Actividad: Corona circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
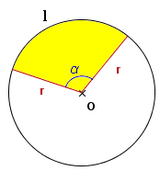
Sector circular
|
|
|
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
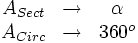
Despejando el área del sector:
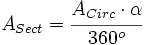
de donde, sustituyendo el área del círculo por su valor, 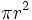 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
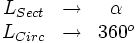
Despejando la longitud del sector:
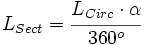
de donde, sustituyendo la longitud de la circunferencia por su valor, 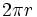 , se obtiene la fórmula.
, se obtiene la fórmula.
|
Actividad interactiva: Sector circular
1. En un círculo de radio 1,80 cm, halla el área de un sector circular de 60º y la longitud de su arco.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de un sector circular
(Mueve el punto B para modificar el ángulo) |
|
Actividad: Sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
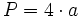
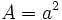
 : lado.
: lado.

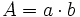
 : base.
: base.
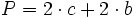
 : lado
: lado
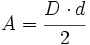

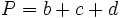
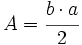
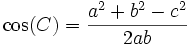
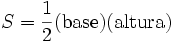
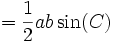
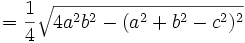
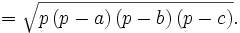
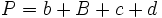
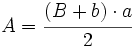
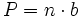
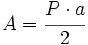
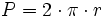
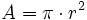
 : número Pi = 3,14159...
: número Pi = 3,14159...
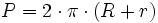
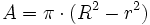
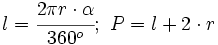
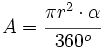
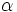 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).

