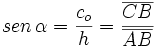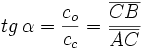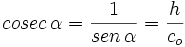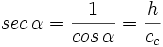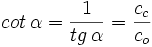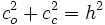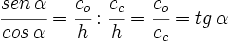Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
| Revisión de 22:35 23 nov 2016 Coordinador (Discusión | contribuciones) (→Relaciones fundamentales de la trigonometría) ← Ir a diferencia anterior |
Revisión de 14:14 24 nov 2016 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de un ángulo agudo) Ir a siguiente diferencia → |
||
| Línea 33: | Línea 33: | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de un ángulo agudo. | + | |descripcion=En esta escena podrás comprobar la realción que hay entre ángulos centrales y ángulos inscritos en una circunferencia. |
| - | |enlace=[https://ggbm.at/hNDCBHEr Razones trigonométricas de un ángulo agudo] | + | |enlace=[https://ggbm.at/AqY3Dnyq Relación entre ángulos centrales e inscritos en una circunferencia] |
| }} | }} | ||
| - | |||
| {{p}} | {{p}} | ||
Revisión de 14:14 24 nov 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
| La trigonometría es una rama de la matemática que estudia las relaciones entre los lados y los ángulos de un triángulo.
Su significado etimológico es la medición de los triángulos, ya que deriva de los términos griegos trigōnos 'triángulo' y metron 'medida'. |
(Pág. 106)
Razones trigonométricas de un ángulo agudo
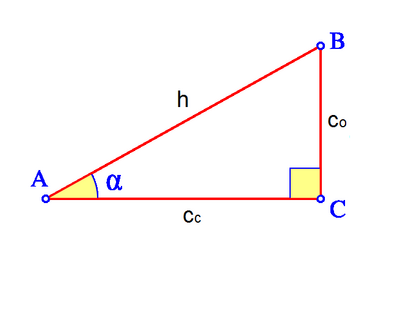
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo agudo  , de la siguiente manera:
, de la siguiente manera:
|
En esta escena podrás comprobar la realción que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
Razones trigonométricas inversas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón inversa del seno:
|
|
- La secante (abreviado como sec), razón inversa del coseno:
|
|
- La cotangente (abreviado como cot), razón inversa de la tangente:
|
|
- Razones trigonométricas de un ángulo agudo.
- Razones trigonométricas inversas.
- Ejemplos.
- Definición razonada de las razones trigonométricas de un ángulo agudo.
En este vídeo jugamos a dibujar un ángulo del que se conoce una de sus seis razones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante).
- Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo.
- Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas.
- Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
Relaciones fundamentales de la trigonometría
Relaciones fundamentales de la trigonometría
1. 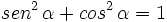
2. 
3. 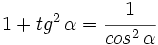
Demostración de las relaciones fundamentales de la trigonometría.
En este vídeo nos dan una de las seis razones trigonométricas de un ángulo y debemos determinar las cinco restantes, haciendo uso de las relaciones fundamentales de la trigonometría.
Ejercicio resuelto: Razones trigonométricas de un ángulo agudo
Sea
 un ángulo agudo.
un ángulo agudo.
- Sabiendo que
 , calcular
, calcular 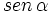 y
y 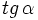 .
.
- Sabiendo que
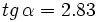 , calcular
, calcular 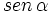 y
y 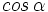 .
.
Hay que usar las relaciones fundamentales de la trigonometría para despejar la razón trigonométrica desconocida:
1. 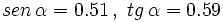
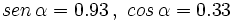
Razones trigonométricas de algunos ángulos importantes
A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar:
| Grados | sen | cos | tg | cosec | sec | cot |
|---|---|---|---|---|---|---|
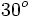
| 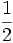
| 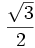
| 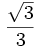
| 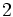
| 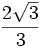
| 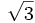
|
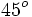
| 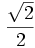
| 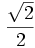
| 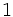
| 
| 
| 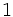
|
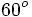
| 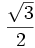
| 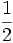
| 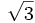
| 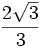
| 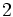
| 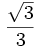
|
En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos.
- Dos ángulos agudos se dicen complementarios si suman 90º.
- El seno de un ángulo agudo coincide con el coseno de su complementario.
- La tangente de un ángulo agudo coincide con la cotangente de su complementario.
- La secante de un ángulo agudo coincide con la cesecante de su complementario.
- Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º.
- También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios.
- Las razones trigonométricas en cuestión deben memorizarse.