Correspondencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:09 8 dic 2016 Coordinador (Discusión | contribuciones) (→Correspondencia entre conjuntos) ← Ir a diferencia anterior |
Revisión de 12:10 8 dic 2016 Coordinador (Discusión | contribuciones) (→Correspondencia entre conjuntos) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| *Al conjunto A se le denomina '''conjunto inicial''' y al B '''conjunto final''' de la correspondencia. | *Al conjunto A se le denomina '''conjunto inicial''' y al B '''conjunto final''' de la correspondencia. | ||
| *Sea <math>x \in A\;</math>, al elemento de B que se corresponda con <math>x\;</math> lo representaremos por <math>f(x)\;</math> y se leerá "''imagen de x según f'' ". (Notación introducida por [[Euler]] en 1734) | *Sea <math>x \in A\;</math>, al elemento de B que se corresponda con <math>x\;</math> lo representaremos por <math>f(x)\;</math> y se leerá "''imagen de x según f'' ". (Notación introducida por [[Euler]] en 1734) | ||
| - | *Al subconjunto de A formado por los elementos que tienen correspondencia con alguno de B, lo llamaremos '''conjunto origen''', <math>Or(f)\;</math>, de la correspondencia f. | + | *Al subconjunto de A formado por los elementos que tienen correspondencia con alguno de B, lo llamaremos '''conjunto origen''', <math>Or(f)\;</math>, de la correspondencia <math>f\;</math>. |
| - | *Al subconjunto de B formado por los elementos que se corresponden con alguno de A, lo llamaremos '''conjunto imagen''', <math>Im(f)\;</math>, de la correspondencia f. | + | *Al subconjunto de B formado por los elementos que se corresponden con alguno de A, lo llamaremos '''conjunto imagen''', <math>Im(f)\;</math>, de la correspondencia <math>f\;</math>. |
| }} | }} | ||
Revisión de 12:10 8 dic 2016
Correspondencia entre conjuntos
Una correspondencia ente dos conjuntos A y B es una ley o criterio que asocia elementos de A con elementos de B.
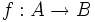
|
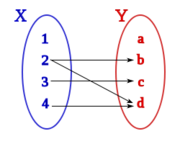
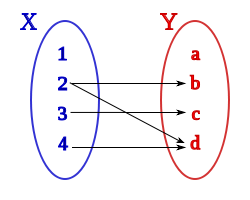
Sean los conjuntos X={1, 2, 3, 4} y Y={a, b, c, d}, una correspondencia entre X e Y podría ser aquella que asocia los elementos de X con los de Y siguiendo el siguiente diagrama de Venn:
- Fíjate que en el conjunto inicial, X, puede haber elementos, {1}, que no tengan asignado ningún elemento del conjunto final, Y.
- Igualmente, puede haber elementos de Y, {a}, a los que no se les ha asignado ningún elemento de X.
- En el conjunto inicial, X, puede haber elementos, {2}, a los que les correspondan más de un elemento de Y.
- Igualmente, puede haber elementos de Y, {d}, a los que les corresponde más de un elmento de X.
- Definición de correspondencia entre conjuntos.
- Conjunto inicial y conjunto final. Ejemplos.
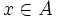 , al elemento de B que se corresponda con
, al elemento de B que se corresponda con  lo representaremos por
lo representaremos por  y se leerá "imagen de x según f ". (Notación introducida por
y se leerá "imagen de x según f ". (Notación introducida por  , de la correspondencia
, de la correspondencia  .
.
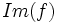 , de la correspondencia
, de la correspondencia