Plantilla:Idea intuitiva de continuidad (1ºBach)
De Wikipedia
| Revisión de 18:33 14 dic 2016 Coordinador (Discusión | contribuciones) (→Discontinuidades) ← Ir a diferencia anterior |
Revisión de 18:43 14 dic 2016 Coordinador (Discusión | contribuciones) (→Discontinuidades) Ir a siguiente diferencia → |
||
| Línea 56: | Línea 56: | ||
| {{p}} | {{p}} | ||
| {{tabla50|celda1={{p}} | {{tabla50|celda1={{p}} | ||
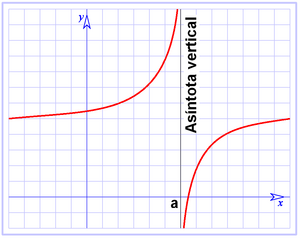
| - | *'''Discontinuidad de salto infinito'''. En este caso la curva tiene alguna "rama infinita" en el punto <math>x=a\;</math>. Decimos que la curva presenta una '''asíntota vertical''' en el punto <math>x=a\;</math>. | + | {{Caja_Amarilla|texto= |
| - | |celda2=<center> | + | '''Discontinuidad de salto finito:''' La función da un salto al llegar a <math>x=a\;</math>. |
| - | [[Imagen:discont_1.png |300 px]]</center> | + | |
| + | Se define el salto como: <math>salto=y_1-y_2\;</math> (ver gráfica adjunta)}} | ||
| + | |celda2=<center>[[Imagen:discont_salto_finito.png |300 px]]</center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{tabla50|celda1={{p}} | {{tabla50|celda1={{p}} | ||
| - | *'''Discontinuidad de salto finito:''' La función da un salto al llegar a <math>x=a\;</math>. En la gráfica adjunta el valor del salto es la diferencia <math>y_1-y_2\;</math>. | + | *'''Discontinuidad de salto infinito'''. En este caso la curva tiene alguna "rama infinita" en el punto <math>x=a\;</math>. Decimos que la curva presenta una '''asíntota vertical''' en el punto <math>x=a\;</math>. |
| - | |celda2=<center>[[Imagen:discont_2.png |300 px]]</center> | + | |celda2=<center> |
| + | [[Imagen:discont_1.png |300 px]]</center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{tabla50|celda1={{p}} | {{tabla50|celda1={{p}} | ||
| + | |||
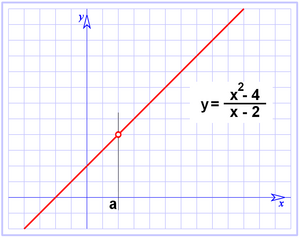
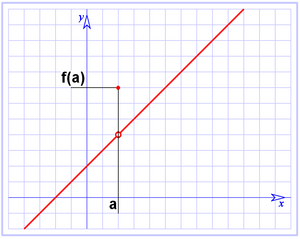
| *'''Discontinuidad evitable (ausencia de punto):''' La función no está definida en el punto <math>x=a\;</math> o bien el punto está desplazado. | *'''Discontinuidad evitable (ausencia de punto):''' La función no está definida en el punto <math>x=a\;</math> o bien el punto está desplazado. | ||
| |celda2= | |celda2= | ||
Revisión de 18:43 14 dic 2016
Idea intuitiva de continuidad
En este apartado pretendemos hacer una acercamiento al concepto de continuidad de una forma intuitiva, sin profundizar y sin usar el concepto de límite, el cual estudiaremos más adelante.
Una función entenderemos que es continua si podemos dibujar su gráfica de un solo trazo. Si en algún punto "se rompe" diremos que presenta una discontinuidad en dicho punto.
Introducción al concepto de continuidad de forma intuitiva. Ejemplo gráfico de discontinuidades.
Propiedad
Las funciones definidas por expresiones analíticas elementales son continuas en todos los puntos de su dominio de definición.
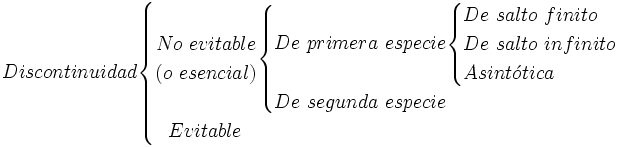
Discontinuidades
Basicamente, nos podemos encontrar los siguientes tipos de discontinuidades en un punto  :
:
|
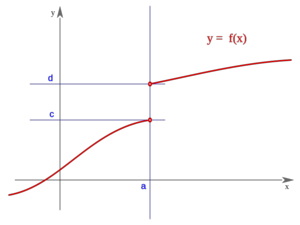
Discontinuidad de salto finito: La función da un salto al llegar a Se define el salto como: |
|
|
|
- Hay otro tipo de discontinuidad, denominada discontinuidad esencial, de la que ya hablaremos cuando veamos el concepto de límite. Entonces formalizaremos el concepto de discontinuidad que aquí hemos visto de forma tan superficial.
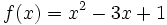 es continua en todos los puntos de su dominio:
es continua en todos los puntos de su dominio: 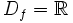 .
.
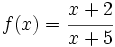 es continua en su dominio:
es continua en su dominio: 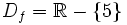 .
.
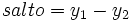 (ver gráfica adjunta)
(ver gráfica adjunta)