Plantilla:Cálculo del límite de una función (1ºBach)
De Wikipedia
| Revisión de 22:00 15 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de una función cuando x tiende a infinito) ← Ir a diferencia anterior |
Revisión de 09:16 17 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de funciones a trozos) Ir a siguiente diferencia → |
||
| Línea 71: | Línea 71: | ||
| {{p}} | {{p}} | ||
| ==Límite de funciones a trozos== | ==Límite de funciones a trozos== | ||
| + | |||
| + | {{Ejemplo|titulo=Ejemplos: ''Estudio de la continuidad de una función definida a trozos'' | ||
| + | |enunciado= | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| - | |titulo1=Estudio de la continuidad de una función a trozos dependiente de parámetros. | + | |titulo1=1. 4 ejemplos |
| + | |duracion=9'41" | ||
| + | |sinopsis=2 ejemplos del estudio de la continuidad de una función definida a trozos con parámetros. | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/17-continuidad-de-funciones/0606-dos-ejemplos-3 | ||
| + | }} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=2. Ejercicio de una una prueba de acceso a la Universidad | ||
| |duracion=7'49" | |duracion=7'49" | ||
| - | |sinopsis=Ejercicio de una una prueba de acceso a la Universidad | + | |sinopsis=Estudio de la continuidad de una función definida a trozos dependiente de parámetros. |
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/05-continuidad-de-funciones/001-ejercicio-5 | |url1=http://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/05-continuidad-de-funciones/001-ejercicio-5 | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Límite de una función en un punto en el que se anula el denominador== | ==Límite de una función en un punto en el que se anula el denominador== | ||
Revisión de 09:16 17 dic 2016
Tabla de contenidos |
Límite en un punto en el que la función es continua
El cálculo de límites de una función en un punto puede ser muy fácil o muy difícil, según los casos. El caso más fácil es cuando la función es continua en dicho punto. En efecto:
Proposición
- Si
 es continua en el punto
es continua en el punto 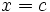 , entonces
, entonces
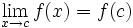
- Es inmediato, por la propia definición de función continua en un punto.
- Recordando el concepto de límite.
Ejemplos: Cálculo de límites
- Cálculo de
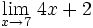
- Cálculo de
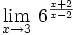
- Cálculo de
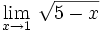
- Cálculo de
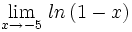
- Cálculo de

- Cálculo de
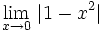
- Cálculo de
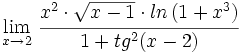
Ejercicios propuestos
|
Ejercicios propuestos: Límite en un punto en el que la función es continua |
Límite de funciones a trozos
Ejemplos: Estudio de la continuidad de una función definida a trozos
2 ejemplos del estudio de la continuidad de una función definida a trozos con parámetros.
Estudio de la continuidad de una función definida a trozos dependiente de parámetros.
{{{sol}}}
Límite de una función en un punto en el que se anula el denominador
Límite de cociente de funciones polinómicas
Paso al límite
El paso al límite como método para calcular límites más complicados
Ejemplos: Paso al límite
Algunos ejemplos de casos sencillos de aplicación de paso al límite.
- Cálculo de límites en una función definida a trozos.
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Ejemplos: Límites infinitos
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com

