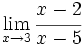Plantilla:Cálculo del límite de una función (1ºBach)
De Wikipedia
| Revisión de 11:08 17 dic 2016 Coordinador (Discusión | contribuciones) (→Límite en un punto en el que la función es continua) ← Ir a diferencia anterior |
Revisión de 11:10 17 dic 2016 Coordinador (Discusión | contribuciones) (→Límite en un punto en el que la función es continua) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| <center><math>\lim_{x \to 3} f(x)=f(3)=\cfrac{3-2}{3-5}=-\cfrac{1}{2}</math></center> | <center><math>\lim_{x \to 3} f(x)=f(3)=\cfrac{3-2}{3-5}=-\cfrac{1}{2}</math></center> | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Cálculo del límite de una función en un punto | ||
| - | |duracion=7'23" | ||
| - | |sinopsis= | ||
| - | Problema típico: te dan la función "f" y te piden que, si existe, calcules su límite en el punto "c". | ||
| - | |||
| - | *'''Límites inofensivos:''' si para calcular f(c) no se viola ninguna Regla Sagrada, la función "f" tiene límite en "c" y coincide con f(c); o sea, existen los dos límites laterales de "f" en "c" y coinciden con f(c). | ||
| - | *'''Límites peligrosos:''' si para calcular f(c) se viola ninguna Regla Sagrada, el cálculo del límite de "f" en "c" puede ser muy complicado, y no hay ninguna receta mágica que resuelva el problema en todos los casos. | ||
| - | |||
| - | No debes olvidar que para calcular el límite en un punto nos importa un pito si la función está o no definida en dicho punto, sólo nos interesa que la función está definida en las proximidades del punto. | ||
| - | |||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/16-limites-de-funciones/04-calculo-de-limites-4 | ||
| - | }} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Paso al límite | ||
| - | |duracion=6'37" | ||
| - | |sinopsis=La operación lógica que llamamos paso al límite (PL) se reduce a conjugar la tercera persona del singular del presente de indicativo del verbo tender. | ||
| - | |||
| - | Recuerda: al escribir x → c (se lee "x" tiende a "c") queremos decir que "x" (o sea, tú) se aproxima a "c" indistintamente por la izquierda o por la derecha. | ||
| - | |||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/02-limites-de-funciones-2/05-paso-al-limite-5 | ||
| - | }} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Operaciones con límites | ||
| - | |duracion=2'33" | ||
| - | |sinopsis=Este vídeo es muy importante: en él hablamos de operaciones con límites, y las efectuaremos constantemente a partir de ahora. | ||
| - | |||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/02-limites-de-funciones-2/06-operaciones-con-limites-4 | ||
| - | }} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{ejemplo2 | {{ejemplo2 | ||
Revisión de 11:10 17 dic 2016
Tabla de contenidos |
Límite en un punto en el que la función es continua
El cálculo de límites de una función en un punto puede ser muy fácil o muy difícil, según los casos. El caso más fácil es cuando la función es continua en dicho punto. En efecto:
Proposición
- Si
 es continua en el punto
es continua en el punto 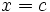 , entonces
, entonces
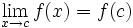
- Es inmediato, por la propia definición de función continua en un punto.
Ejemplo: Cálculo del límite en un punto en el que la función es continua
Calcula:
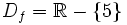 y sabemos que la función es continua en su dominio por ser una función elemental (cociente de funciones polinómicas).
y sabemos que la función es continua en su dominio por ser una función elemental (cociente de funciones polinómicas).
Como 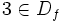 , entonces
, entonces  es continua en 3 y, por tanto:
es continua en 3 y, por tanto:
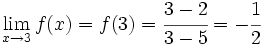
Ejemplos: Cálculo del límite en un punto en el que la función es continua
- Cálculo de
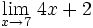
- Cálculo de
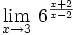
- Cálculo de
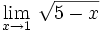
- Cálculo de
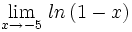
- Cálculo de

- Cálculo de
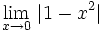
- Cálculo de
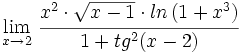
Ejercicios propuestos
|
Ejercicios propuestos: Límite en un punto en el que la función es continua |
Límite de funciones a trozos
Ejemplos: Estudio de la continuidad de una función definida a trozos
2 ejemplos del estudio de la continuidad de una función definida a trozos con parámetros.
Estudio de la continuidad de una función definida a trozos con parámetros.
{{{sol}}}
Límite de una función en un punto en el que se anula el denominador
Límite de cociente de funciones polinómicas
Paso al límite
El paso al límite como método para calcular límites más complicados
Ejemplos: Paso al límite
Algunos ejemplos de casos sencillos de aplicación de paso al límite.
- Cálculo de límites en una función definida a trozos.
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Ejemplos: Límites infinitos
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com