Plantilla:Ramas infinitas. Asíntotas (1ºBach)
De Wikipedia
| Revisión de 17:13 18 dic 2016 Coordinador (Discusión | contribuciones) (→Asíntotas) ← Ir a diferencia anterior |
Revisión de 17:13 18 dic 2016 Coordinador (Discusión | contribuciones) (→Asíntotas) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Asíntotas== | ==Asíntotas== | ||
| - | {{Caja_Amarilla|texto=Las '''asíntotas''' son rectas hacia las que se acerca la gráfica de una recta, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto o a <math>+ \infty</math> o a <math>-\infty</math>.}} | + | {{Caja_Amarilla|texto=Las '''asíntotas''' son rectas hacia las que se acerca la gráfica de una recta, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto, a <math>+ \infty</math> o a <math>-\infty</math>.}} |
| {{p}} | {{p}} | ||
| ===Asíntotas verticales=== | ===Asíntotas verticales=== | ||
Revisión de 17:13 18 dic 2016
Tabla de contenidos |
Asíntotas
Las asíntotas son rectas hacia las que se acerca la gráfica de una recta, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto, a  o a
o a  .
.
Asíntotas verticales
Una función La gráfica de la función se acerca a la recta | Asíntota vertical: x = 2
|
Asíntotas horizontales
Una función | Asíntota horizontal: y = 1</math>
|
Asíntotas oblicuas
Una función Para calcular los coeficientes
| Asíntota oblicua: y = 2x + 6
|
Ramas infinitas
Una función f(x) presenta una rama infinita si ocurre uno de los dos casos siguientes:
| Ramas infinitas que no son asíntotas
|
Ramas infinitas cuando x tiene a infinito
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas |
Ramas infinitas de las funciones racionales
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones racionales |
Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas |
 presenta en
presenta en  una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
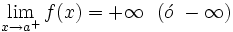
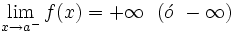
 al punto
al punto 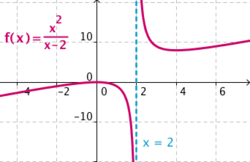
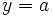 si ocurre alguna, o ambas, de estas dos cosas:
si ocurre alguna, o ambas, de estas dos cosas:
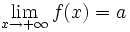
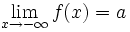

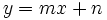 si ocurre alguna, o ambas, de estas dos cosas:
si ocurre alguna, o ambas, de estas dos cosas:
![\lim_{x \to +\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/b/4/f/b4f57eb5b14023e40e6485b640fd5691.png)
![\lim_{x \to -\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/d/c/1/dc195dc202ab07f6f60038a1570d06b3.png)
 y
y  de la asíntota, se procederá de la siguiente manera:
de la asíntota, se procederá de la siguiente manera:
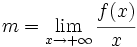 (o con
(o con 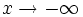 )
)
![n=\lim_{x \to +\infty} [f(x)-mx]](/wikipedia/images/math/c/d/7/cd758129321f1a26b36d644470fd76f5.png) (o con
(o con 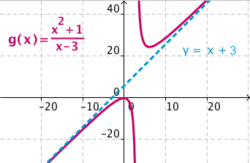
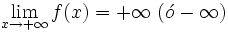 , o bien,
, o bien, 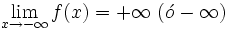 .
.