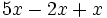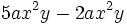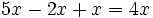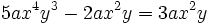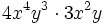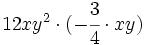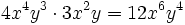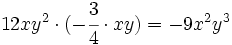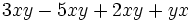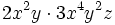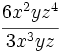Plantilla:Operaciones con monomios
De Wikipedia
| Revisión de 10:18 7 feb 2017 Coordinador (Discusión | contribuciones) (→Suma y resta de monomios) ← Ir a diferencia anterior |
Revisión de 10:50 7 feb 2017 Coordinador (Discusión | contribuciones) (→Producto de monomios) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| ===Producto de monomios=== | ===Producto de monomios=== | ||
| - | Recordemos que para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes. Así, para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican. | + | {{producto de monomios}} |
| - | {{p}} | + | |
| - | {{Ejemplo | + | |
| - | |titulo=Ejemplos: ''Producto de monomios'' | + | |
| - | |enunciado= | + | |
| - | Calcula: | + | |
| - | + | ||
| - | :a) <math>4ax^4y^3 \cdot x^2y \cdot 3ab^2y^3 \;\!</math> | + | |
| - | + | ||
| - | :b) <math>2ax^2 \cdot (-3a^3x) \cdot 5y^4x^3 \;\!</math> | + | |
| - | |sol= | + | |
| - | a) <math>4ax^4y^3 \cdot x^2y \cdot 3ab^2y^3 = 12a^2b^2x^6y^7 \;\!</math> | + | |
| - | + | ||
| - | b) <math>2ax^2 \cdot (-3a^3x) \cdot 5y^4x^3 = -30 a^4x^6y^4 \;\!</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión de 10:50 7 feb 2017
Suma y resta de monomios
Procedimiento
Para sumar o restar dos monomios tienen que ser semejantes. La suma o resta es otro monomio semejante a ellos que tiene por coeficiente la suma o diferencia, según el caso, de los coeficientes.
Suma y resta de monomios. Monomios opuestos.
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Agrupa (reduce) términos semejantes:
a) 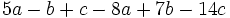
b) 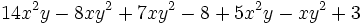
Reduce:
a) 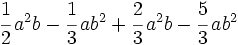
b) 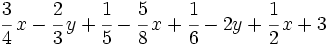
Realiza las siguientes sumas y restas de monomios:
- 22)
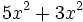 ; 23)
; 23) 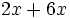 ; 24)
; 24) 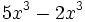
- 25)
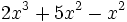 ; 26)
; 26) 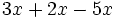 ; 27)
; 27) 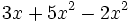
- 28)
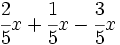 ; 29)
; 29)  ; 30)
; 30) 
- 31)
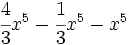 ; 32)
; 32) 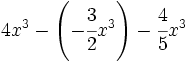
Actividades en la que aprenderás y practicarás a sumar y restar monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Producto de monomios
Procedimiento
Para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican.
Recordemos que: para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes.
Multiplicación de monomios. Ejemplos.
Haz las siguientes multiplicaciones de monomios:
- a)
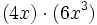
- b)
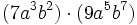
- c)
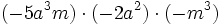
Haz las siguientes multiplicaciones de monomios:
- a)
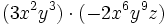
- b)
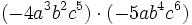
- c)
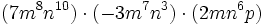
- d)
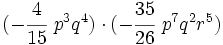
Haz las siguientes multiplicaciones de monomios:
- a)
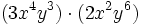
- b)
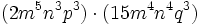
- c)
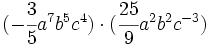
Multiplica los siguientes monomios:
- 37)
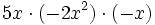 ; 38)
; 38) 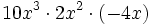 ; 39)
; 39) 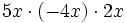
- 40)
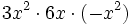 ; 41)
; 41) 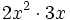 ; 42)
; 42) 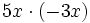
- 43)
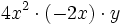 ; 44)
; 44) 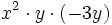
Multiplica los siguientes monomios:
- 45)
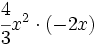 ; 46)
; 46) 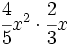 ; 47)
; 47) 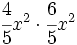
- 48)
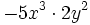 ; 49)
; 49) 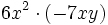 ; 50)
; 50) 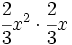
- 51)
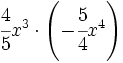 ; 52)
; 52) 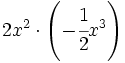 ; 53)
; 53) 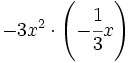
Expresa en forma de un monomio el área de un rectángulo que mide 4y de largo y 2y de ancho.
Expresa en forma de un monomio el área de un rectángulo que mide 4xy de largo y 2y de ancho.
Averigua el valor de "a" y "b" sabiendo que 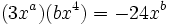 .
.
Actividades en la que aprenderás y practicarás a multiplicar monomios.
Actividades para practicar la multiplicación de monomios.
Multiplicación de monomios.
Multiplicación de monomios.
División de monomios
Entenderemos la división como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Ejemplos: División de monomios
Calcula:
- a)
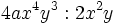
- b)
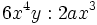
a) 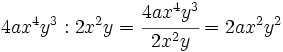
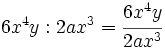 . No es posible la división pues no hay
. No es posible la división pues no hay  en el numerador.
en el numerador.