Plantilla:Teorema de Tales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:43 7 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:48 7 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 40: | Línea 40: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo | ||
| - | |titulo=Proposición | ||
| - | |enunciado=En las condiciones del teorema de Tales, tabién se cumplen las siguientes relaciones: | ||
| - | {{b}} | ||
| - | {{p}} | ||
| - | <center><math> \frac {\overline{OA}} {\overline{OA'}} = \frac {\overline{OB}} {\overline{OB'}} = \frac {\overline{AB}} {\overline{A'B'}}</math></center> | ||
| - | {{p}} | ||
| - | En consecuencia, los triángulos OAB y OA'B' son semejantes. | ||
| - | }} | ||
Revisión de 10:48 7 may 2017
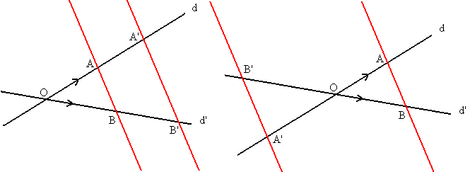
Primer teorema de Tales
| Dos rectas paralelas, AB y A'B', que cortan a dos rectas secantes, d y d', determinan en éstas segmentos proporcionales:
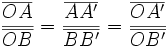 |
Demostración:
Demostración del primer teorema de Thales.
Ejemplo de aplicación del primer teorema de Thales.
Ejercicio de aplicación del primer teorema de Thales.
En esta escena podrás comprobar el primer teorema de Tales.