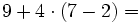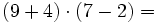Biblioteca de plantillas
De Wikipedia
| Revisión de 11:35 6 may 2017 Coordinador (Discusión | contribuciones) (→Video1) ← Ir a diferencia anterior |
Revisión de 18:57 7 may 2017 Coordinador (Discusión | contribuciones) (→Video enlace unicoos) Ir a siguiente diferencia → |
||
| Línea 175: | Línea 175: | ||
| |url1=http://www.unicoos.com/video/matematicas/1-bachiller/funciones/caracteristicas-basicas/dominio-de-una-funcion | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/funciones/caracteristicas-basicas/dominio-de-una-funcion | ||
| }} | }} | ||
| + | ===Video enlace carreon=== | ||
| + | {{p}} | ||
| + | {{Video_enlace_carreon | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=5´15" | ||
| + | |sinopsis=Sucesiones con figuras | ||
| + | |url1=https://www.youtube.com/watch?v=SPJwfXwwaOg}} | ||
| + | |||
| + | {{p}} | ||
| + | |||
| ===Video enlace julioprofe=== | ===Video enlace julioprofe=== | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
Revisión de 18:57 7 may 2017
Tabla de contenidos |
Menús
Menú Desplegable
| Ir a | Para repasar | Para ampliar | Herramientas |
| Indice | Tablas multiplicar | Números naturales | WIRIS |
Menú Derecha
| NUMEROS NATURALES |
| Ir a |
| Para ampliar |
| Para repasar |
| Herramientas |
Menú Asignatura
| Enlaces |
| Descartes WIRIS Geometría (E.S.O.) |
| Ejercicios |
| E.S.O. Bachillerato |
| Multimedia |
| {{{multimedia}}} |
| Documentos |
| Exámenes Programaciones |
Tablas
Tablabonita
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tablabonitablanca
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tabla75
| 1 | 2 |
Tabla50
| 1 | 2 |
Tabla3
| 1 | 2 | 3 |
Tabla3b
| 1 | 2 | 3 |
Tabla4
| 1 | 2 | 3 | 4 |
Wiris
Wolfram
|
Actividad: Opuesto de un número entero a) Calcula el opuesto de 3 b) Calcula el opuesto de -5 Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) opposite 3 b) opposite -5 |
Video
Video enlace
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video enlace 2
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video enlace unicoos
- 5 ejemplos.
Video enlace carreon
Sucesiones con figuras
Video enlace julioprofe
- Suma de polinomios.
Video enlace fonemato
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
Videotutoriales
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
- Definición de producto de números complejos en forma binómica.
- Ejemplos.
- Propiedades.
- Definición de cociente de números complejos en forma binómica.
- Ejemplos.
Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en forma polar como se verá en otro apartado de este tema.
Video1
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2b
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Web
{{{descripcion}}}
Web: Phi el número de oro
Web de Luis Nicolás Ortiz.
Geogebra
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
MP3
Calculadora
|
Calculadora: Notación científica |
Calculadora2
|
{{{titulo}}} {{{cuerpo}}} |
Teoremas
Teorema
Teorema sin demo
Ejemplos
Ejemplo_simple (sin caja)
Ejemplo (con solución)
Ejemplo2 (sin solución)
Ejemplos múltiples
Ejemplos: Ecuaciones trigonométricas
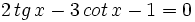
Transformamos la ecuación de partida:
Hacemos un cambio de variable: 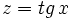
Soluciones:
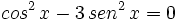
Usando la identidad fundamental:
Sustituimos en nuestra ecuación de partida:
Soluciones:
Compositores
Ejercicios
Actividad (sin solución)
|
Actividad 1
|
Wolfram
|
Actividad: Valor numérico de una expresión algebraica |
Wolfram con widget
|
Actividad: Operaciones aritméticas 1. Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Wolfram desplegable
Ejercicios (con solución)
|
Ejercicios 1. Calcula:
Solución: a) 35 b) 89 c) 29 d) 65
2. En una división, el dividendo es 969, el cociente 74, y el resto 7. ¿Cúal es el divisor?
Solución: El divisor es 13 |
Ecuación (con número de referencia)
| Aquí vendría la fórmula | (Num. Ref.) |
Cajas
Caja Amarilla
Este es el contenido
Caja Naranjaa
Este es el contenido
Caja
|
Aquí vendría la fórmula |
Actividad interactiva
AI enlace
Un poco de historia sobre el papiro de Rhind. Las fracciones unitarias.
AI
AI2
|
Actividades Interactivas: Formas de expresar una función
1. Variable discreta.
Actividad:
2. Variable continua.
Actividad: El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas. |
AI3
Desplegables
Desplegable
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Desplegable2
Sea AB un diámetro de la circunferencia: 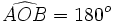 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 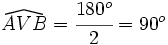 .
.
Tarea
Eventos calendario
Sintaxis:
{{Evento
|tipo=Puede ser uno de los 4 siguientes: Tarea, Examen, Act.Extraescolar, Otros
|asignatura=Asignatura
|contenido=Explicación del evento
}}
Ejemplos

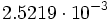

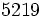

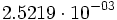
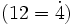 porque
porque 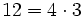 . Por tanto, 4 es divisor de 12
. Por tanto, 4 es divisor de 12 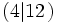 .
.
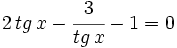
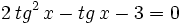
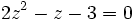
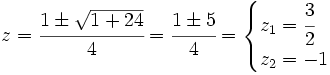
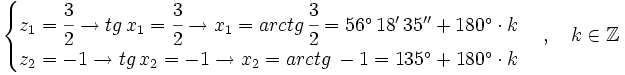
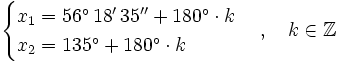
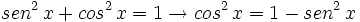
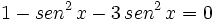
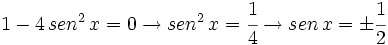
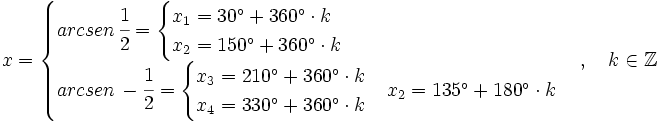
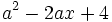 en los casos:
en los casos: