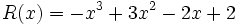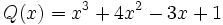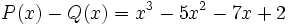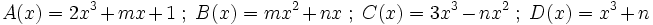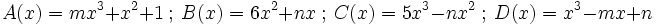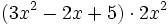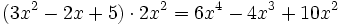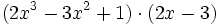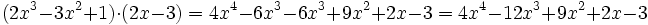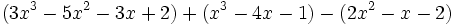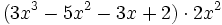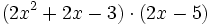Plantilla:Operaciones con polinomios

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 10:21 15 may 2017

Suma y resta de polinomios

Procedimiento

Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.

Ejemplos: Suma y resta de polinomios

Calcula:

a) $(3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) \;\!$

b) $(3x^2 - 2x + 5 ) - ( x^2 + 2x) \;\!$

Solución:

a) $(3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) = 5x^3+2x^2+5 \;\!$

b) $(3x^2 - 2x + 5 ) - (x^2 + 2x ) = 2x^2-4x+5 \;\!$

Suma y resta de polinomios

Tutorial 1 (7'35") Sinopsis:

Aprende a sumar y restar polinomios

Tutorial 2 (23'12") Sinopsis:

En este tutorial se explica la suma y resta de polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.

Tutorial 3a (Suma) (4'09") Sinopsis:

Aprende a sumar polinomios

Tutorial 3b (Resta) (4'37") Sinopsis:

Aprende a restar polinomios

Tutorial 4 (6'57") Sinopsis:

Suma y resta de polinomios en una variable. Ejemplos.

Tutorial 5a (Suma) (12'33") Sinopsis:

Suma de polinomios. Ejemplos.

Tutorial 5b (Propiedades de la suma I) (14'39") Sinopsis:

Propiedades de la suma de polinomios: conmutativa y asociativa.

Tutorial 5c (Propiedades de la suma II) (5'40") Sinopsis:

Propiedades de la suma de polinomios: Elemento neutro y opuesto.

Tutorial 5d (Resta) (7'58") Sinopsis:

Resta de polinomios. Equivalencias fundamentales.

Tutorial 6 (9'25") Sinopsis:

Suma y resta de polinomios.

Ejercicio 1 (2'55") Sinopsis:

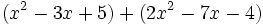
Calcula la suma: $(x^2-3x+5)+(2x^2-7x-4)\,$

Ejercicio 2 (3'15") Sinopsis:

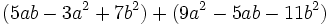
Calcula la suma: $(5ab-3a^2+7b^2)+(9a^2-5ab-11b^2)\,$

Ejercicio 3 (2'51") Sinopsis:

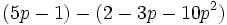
Calcula la resta: $(5p-1)-(2-3p-10p^2)\,$

Ejercicio 4 (6'27") Sinopsis:

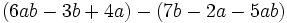
Calcula la resta: $(6ab-3b+4a)-(7b-2a-5ab)\,$

Ejercicio 5 (8'56") Sinopsis:

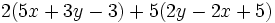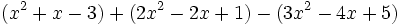
Calcula: a) $2(5x+3y-3)+5(2y-2x+5)\,$ b) $(x^2+x-3)+(2x^2-2x+1)-(3x^2-4x+5)\,$

Ejercicio 6a (3'29") Sinopsis:

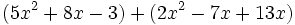
Simplifica: $(5x^2+8x-3)+(2x^2-7x+13x)\;$

Ejercicio 6b (2'17") Sinopsis:

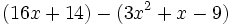
Simplifica: $(16x+14)-(3x^2+x-9)\;$

Ejercicio 6c (7'38") Sinopsis:

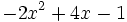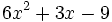Resta $-2x^2+4x-1\;$ de $6x^2+3x-9\;$ .

Ejercicio 6d (3'57") Sinopsis:

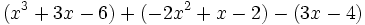
Simplifica: $(x^3+3x-6)+(-2x^2+x-2)-(3x-4)\;$

Ejercicio 6e (3'07") Sinopsis:

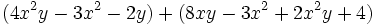
Simplifica: $(4x^2y-3x^2-2y)+(8xy-3x^2+2x^2y+4)\;$

Ejercicio 6f (2'47") Sinopsis:

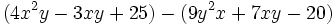
Simplifica: $(4x^2y-3xy+25)-(9y^2x+7xy-20)\;$

Ejercicio 6g (4'14") Sinopsis:

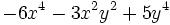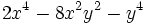Resta $-6x^4-3x^2y^2+5y^4\;$ de $2x^4-8x^2y^2-y^4\;$ .

Ejercicio 6h (2'52") Sinopsis:

Encuentra el error cometido en la resta que se muestra en el video.

Ejercicio 7a (13'40") Sinopsis:

1) Ordena los polinomios y realiza las sumas que se indican:

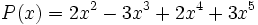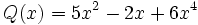
$P(x)=2x^2-3x^3+2x^4+3x^5\;$ ; $Q(x)=5x^2-2x+6x^4\;$

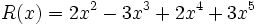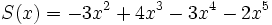
$R(x)=2x^2-3x^3+2x^4+3x^5\;$ ; $S(x)=-3x^2+4x^3-3x^4-2x^5\;$

1a) P(x) + Q(x)

1b) P(x) + R(x)

1c) P(x) + S(x)

Ejercicio 7b (10'49") Sinopsis:

Dados los siguientes polinomios, realiza las sumas que se indican:

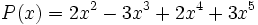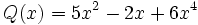
$P(x)=2x^2-3x^3+2x^4+3x^5\;$ ; $Q(x)=5x^2-2x+6x^4\;$

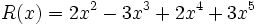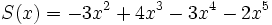
$R(x)=2x^2-3x^3+2x^4+3x^5\;$ ; $S(x)=-3x^2+4x^3-3x^4-2x^5\;$

1d) Q(x) + S(x)

1e) R(x) + S(x)

1f) Q(x) + R(x)

Ejercicio 8a (17'35") Sinopsis:

2) Sumas los siguientes polinomios y compara el grado del polinomio suma con el grado de los polinomios sumandos.

$R(x)=-x^3+3x^2-2x+2\;$

$Q(x)=x^3+4x^2-3x+1\;$

3a) Escribe opuestos de los siguientes polinomios:

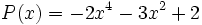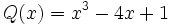
$P(x)=-2x^4-3x^2+2\;$ ; $Q(x)=x^3-4x+1\;$

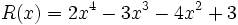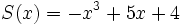
$R(x)=2x^4-3x^3-4x^2+3\;$ ; $S(x)=-x^3+5x+4\;$

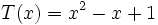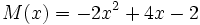
$T(x)=x^2-x+1\;$ ; $M(x)=-2x^2+4x-2\;$

3b) Suma cada uno de los polinomios del apartado anterior con su opuesto.

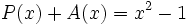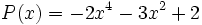3c) Calcula un polinomio A(x) tal que $P(x)+A(x)=x^2-1\;$ , siendo $P(x)=-2x^4-3x^2+2\;$ .

Ejercicio 8b (16'45") Sinopsis:

Dados los siguientes polinomios:

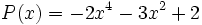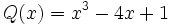
$P(x)=-2x^4-3x^2+2\;$ ; $Q(x)=x^3-4x+1\;$

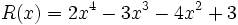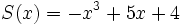
$R(x)=2x^4-3x^3-4x^2+3\;$ ; $S(x)=-x^3+5x+4\;$

3d) Calcula un polinomio B(x) tal que 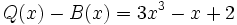$Q(x)-B(x)=3x^3-x+2\;$ .

3e) Calcula un polinomio C(x) tal que 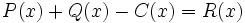$P(x)+Q(x)-C(x)=R(x)\;$ .

3f) Calcula un polinomio D(x) tal que 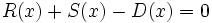$R(x)+S(x)-D(x)=0\;$ .

Ejercicio 9 (12'30") Sinopsis:

Dados los polinomios:

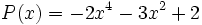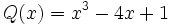
$P(x)=-2x^4-3x^2+2\;$ ; $Q(x)=x^3-4x+1\;$

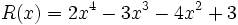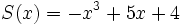
$R(x)=2x^4-3x^3-4x^2+3\;$ ; $S(x)=-x^3+5x+4\;$

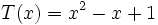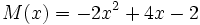
$T(x)=x^2-x+1\;$ ; $M(x)=-2x^2+4x-2\;$

4a) Calcula P(x) - Q(x).

4b) Calcula P(x) - R(x).

4c) Calcula [P(x) + Q(x)]-[R(x) + S(x)]

4d) Calcula [P(x) + S(x)]-[Q(x) + R(x)]

4e) Calcula T(x) + M(x)

4f) Calcula T(x) - M(x)

Ejercicio 10 (16'53") Sinopsis:

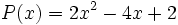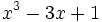5) ¿Qué polinomio se ha de restar al polinomio $P(x)=2x^2-4x+2\;$ para obtener el polinomio $x^3-3x+1\;$ ?

6) Dados los polinomios

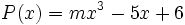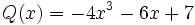
$P(x)=mx^3-5x+6\;$ ; $Q(x)=-4x^3-6x+7\;$

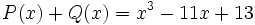calcula el valor de $m\;$ sabiendo que $P(x)+Q(x)=x^3-11x+13\;$ .

7) Escribe dos polinomios de tercer grado de tal modo que su suma se el polinomio nulo.

8) Escribe dos polinomios reducidos de segundo grado y comprueba con ellos la conmutatividad de la suma.

Ejercicio 11 (14'20") Sinopsis:

9) Dado el polinomio 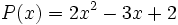$P(x)=2x^2-3x+2\;$ , escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.

10) ¿Qué polinomio tienes que sumar con 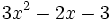$3x^2-2x-3\;$ para que la suma sea 5x^3-6x?

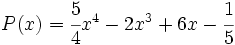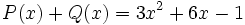11) Dado el polinomio $P(x)=\cfrac{5}{4}x^4-2x^3+6x-\cfrac{1}{5}\;$ , halla otro polinomio Q(x) tal que $P(x)+Q(x)=3x^2+6x-1\;$ .

Ejercicio 12 (7'27") Sinopsis:

Dados los polinomios

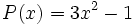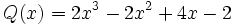
$P(x)=3x^2-1\;$ ; $Q(x)=2x^3-2x^2+4x-2\;$

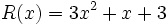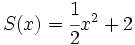
$R(x)=3x^2+x+3\;$ ; $S(x)=\cfrac{1}{2}x^2+2\;$

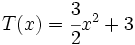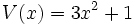
$T(x)=\cfrac{3}{2}x^2+3\;$ ; $V(x)=3x^2+1\;$

12a) Calcula P(x) + Q(x).

12b) Calcula P(x) - V(x).

12c) Calcula P(x) + R(x).

12d) Calcula P(x) - R(x).

12e) Calcula S(x) + T(x) + V(x).

12f) Calcula S(x) - T(x) + V(x).

Ejercicio 13 (11'55") Sinopsis:

13) Dados los polinomios

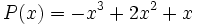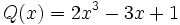
$P(x)=-x^3+2x^2+x\;$ ; $Q(x)=2x^3-3x+1\;$

calcula el polinomio M(x) tal que P(x) + M(x) = Q(x).

Ejercicio 14 (15'13") Sinopsis:

17) La diferencia de dos polinomios es:

$P(x)-Q(x)=x^3-5x^2-7x+2\;$

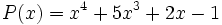Calcula $Q(x)\;$ sabiendo que $P(x)=x^4+5x^3+2x-1\;$ .

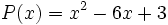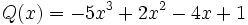18) ¿Qué polinomio hay que sumar al polinomio $P(x)=x^2-6x+3\;$ para obtener el polinomio opuesto de $Q(x)=-5x^3+2x^2-4x+1\;$ ?

19) Dados los polinomios:

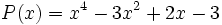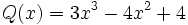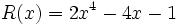
$P(x)=x^4-3x^2+2x-3\;$ ; $Q(x)=3x^3-4x^2+4\;$ ; $R(x)=2x^4-4x-1\;$

19a) Calcula P(x) + Q(x) - R(x)

19b) Calcula P(x) + R(x) - Q(x)

19c) Calcula Q(x) + R(x) - P(x)

19d) Calcula P(x) + Q(x) + R(x)

14) Escribe dos polinomios cualesquiera y súmalos. Contesta:

14a) ¿Es mayor el grado de los sumandos o el de la suma? ¿Es igual? ¿Es menor?

14b) ¿Puede en algún caso ser menor el grado de la suma que el de los sumandos? ¿Cuándo? Justifícalo con ejemplos.

15) ¿Qué puedes decir del grado de la diferencia de dos polinomios?

16) escribe dos polinomios de tercer grado de modo que su suma se el polinomio 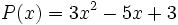$P(x)=3x^2-5x+3\;$ .

Ejercicio 15 (6'49") Sinopsis:

Determina el valor de "m" y "n" sabiendo que 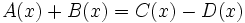$A(x)+B(x) = C(x)-D(x)\;$ , en los siguientes casos:

$A(x)=2x^3+mx+1 \ ; \ B(x)=mx^2+nx \ ; \ C(x)=3x^3-nx^2 \ ; \ D(x)=x^3+n$
$A(x)=mx^3+x^2+1 \ ; \ B(x)=6x^2+nx \ ; \ C(x)=5x^3-nx^2 \ ; \ D(x)=x^3-mx+n$

Suma y resta de polinomios

Actividad 1 Descripción:

Actividades para aprender y practicar la suma y resta de polinomios.

Actividad 2 Descripción:

Ejercicios para practicar la suma y resta de polinomios.

Autoevaluación 1a (suma) Descripción:

Suma de polinomios.

Autoevaluación 1b (resta) Descripción:

Resta de polinomios.

Autoevaluación 1c Descripción:

Suma y resta de polinomios.

Autoevaluación 1d Descripción:

Suma y resta de polinomios con dos variables.

Autoevaluación 1e Descripción:

Suma y resta de polinomios con dos variables.

Autoevaluación 1f Descripción:

Suma y resta de polinomios con dos variables: encuentra el error.

Autoevaluación 2a (suma) Descripción:

Suma de polinomios.

Autoevaluación 2b (resta) Descripción:

Resta de polinomios.

Autoevaluación 3 Descripción:

Ejercicios de autoevaluación sobre suma y resta de polinomios.

Producto de un monomio por un polinomio

Procedimiento

Para multiplicar un monomio por un polinomio, se aplica la propiedad distributiva, es decir, se multiplica el monomio por cada término del polinomio y se suman los resultados.

Ejemplo: Producto de un monomio por un polinomio

Calcula el producto: $(3x^2 - 2x + 5 ) \cdot 2x^2 \;\!$

Solución:

$( 3x^2 - 2x + 5 ) \cdot 2x^2 = 6x^4-4x^3+10x^2 \;\!$

Producto de un monomio por un polinomio

Tutorial 1 (12'28") Sinopsis:

Aprende a multiplicar un monomio por un polinomio

Tutorial 2 (6'19") Sinopsis:

Cómo se multiplica un polinomio por un monomio.

Ejercicio 1a (4'08") Sinopsis:

Multiplica y reduce:

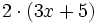
a) $2 \cdot (3x+5)\;$

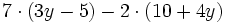
b) $7 \cdot (3y-5) - 2 \cdot (10+4y)\;$

Ejercicio 1b (2'06") Sinopsis:

Expresa el área de la figura dada en el video como un trinomio.

Ejercicio 1c (2'38") Sinopsis:

Multiplica: 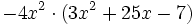$-4x^2 \cdot (3x^2+25x-7)\;$

Ejercicio 1d (5'31") Sinopsis:

Averigua el valor de "c", "d" y "f" sabiendo que 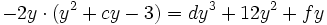$-2y \cdot (y^2+cy-3)=dy^3+12y^2+fy\;$

Ejercicio 2 (7'07") Sinopsis:

Multiplica:

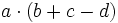
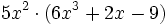
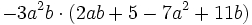
a) $a \cdot (b+c-d)\;$

b) $5x^2 \cdot (6x^3+2x-9)\;$

c) $-3a^2b \cdot (2ab+5-7a^2+11b)\;$

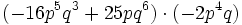
d) $(-16p^5q^3+25pq^6) \cdot (-2p^4q)\;$

Ejercicio 3 (8'21") Sinopsis:

Haz las siguientes multiplicaciones de monomios:

a) $a(x-y+z)\,$

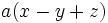
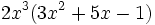
b) $2x^3(3x^2+5x-1)\,$

c) $3x^2 \cdot 2y^3(-3x^2+4xy-2y^2)\,$

Ejercicio 4a (8'55") Sinopsis:

Calcula $(x^4 +2x^3+x^2-2x+2) \cdot (\cfrac{1}{2}x)\,$

Ejercicio 4b (7'19") Sinopsis: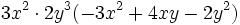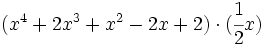

Calcula:

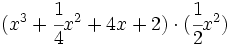
1c) $(x^3 +\cfrac{1}{4}x^2+4x+2) \cdot (\cfrac{1}{2}x^2)\,$

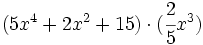
1d) $(5x^4 +2x^2+15) \cdot (\cfrac{2}{5}x^3)\,$

Producto de monomio por polinomio

Actividad Descripción:

Actividades para aprender y practicar la multiplicación de un monomio por un polinomio.

Autoevaluación 1 Descripción:

Multiplicación de un número por un polinomio.

Autoevaluación 2 Descripción:

Multiplicación de monomios por polinomios.

Autoevaluación 3 Descripción:

Multiplicación de monomios por polinomios.

Autoevaluación 4 Descripción:

Multiplicación de monomios por polinomios.

Producto de polinomios

Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.

Ejemplo: Producto de polinomios

Calcula el producto: $(2x^3 - 3x^2 +1) \cdot (2x-3)\;\!$

Solución:

$(2x^3 - 3x^2 +1) \cdot (2x-3) = 4x^4-6x^3-6x^3+9x^2+2x-3=4x^4-12x^3+9x^2+2x-3 \;\!$

{{Videotutoriales|titulo=Producto de polinomios|enunciado=

Ejemplos 1: Producto de binomios (7'55") Sinopsis:

Aprende a multiplicar binomios

Ejemplos 2: Producto de polinomios (11'43") Sinopsis:

Multiplica:

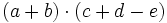
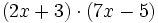
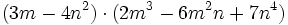
a) $(a+b) \cdot (c+d-e)\;$

b) $(2x+3) \cdot (7x-5)\;$

c) $(3m-4n^2) \cdot (2m^3-6m^2n+7n^4)\;$

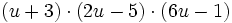
d) $(u+3) \cdot (2u-5)\cdot (6u-1)\;$

[https://www.youtube.com/watch?v=bQujBEvDlk4

Problema (5') Sinopsis:

Determinar el polinomio que tiene por raíces: 2, 3 y -1, siendo la última raíz de multiplicidad 2.

Ejemplos 3: Producto de polinomios] (10'46") Sinopsis:

3 ejemplos

Operaciones con polinomios

Actividad: Operaciones con polinomios

Haz las siguientes operaciones con polinomios:

a) $(3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2)\!$

b) $(3x^3-5x^2-3x+2) \cdot 2x^2\!$

c) $(2x^2+2x-3) \cdot (2x-5)\!$

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2) b) expand (3x^3-5x^2-3x+2)*2x^2 c) expand (2x^2+2x-3)*(2x-5)

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Operaciones_con_polinomios"

 |url1=https://www.youtube.com/watch?v=xRC447bTueU}}
+{{p}}
+{{Video_enlace
+|titulo1=Ejemplos 3: ''Producto de polinomios''
+|duracion=10'46"
+|sinopsis=3 ejemplos
+|url1=https://www.youtube.com/watch?v=bQujBEvDlk4
 {{p}}
 {{Video_enlace_julioprofe

Plantilla:Operaciones con polinomios

De Wikipedia

Revisión de 10:21 15 may 2017

Suma y resta de polinomios

Producto de un monomio por un polinomio

Producto de polinomios

Vistas

Herramientas personales

Menú

Buscar

Herramientas