Plantilla:Derivada (1ºBach)
De Wikipedia
| Revisión de 09:31 8 may 2017 Coordinador (Discusión | contribuciones) (→Obtención de la derivada de una función en un punto) ← Ir a diferencia anterior |
Revisión de 06:03 17 may 2017 Coordinador (Discusión | contribuciones) (→Obtención de la derivada de una función en un punto) Ir a siguiente diferencia → |
||
| Línea 28: | Línea 28: | ||
| |descripcion=En esta escena podrás ver cómo se interpreta geométricamente el concepto de derivada de una función en un punto. | |descripcion=En esta escena podrás ver cómo se interpreta geométricamente el concepto de derivada de una función en un punto. | ||
| |enlace=[https://ggbm.at/hgCkgeU8 Derivada de una función en un punto] | |enlace=[https://ggbm.at/hgCkgeU8 Derivada de una función en un punto] | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo: Derivada de una función en un punto | ||
| - | |duracion=9'24" | ||
| - | |sinopsis=En la segunda parte de este video podrás ver un ejemplo de derivada de una función en un punto usando la definición de derivada. | ||
| - | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/derivadas/definicion-de-derivada/derivada-utilizando-la-definicion-01 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 06:03 17 may 2017
Tabla de contenidos |
Crecimiento de una función en un punto. Derivada
- El crecimiento de una función
 en un intervalo
en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) se mide mediante la pendiente de la recta que pasa por los puntos
se mide mediante la pendiente de la recta que pasa por los puntos 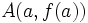 y
y 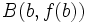 , es decir, mediante
, es decir, mediante ![T.V.M._f[a,b]\;](/wikipedia/images/math/1/b/0/1b099a5cc384e6e5cd2dce91dc815fa8.png) .
.
- El crecimiento de una función
 en un punto de abscisa
en un punto de abscisa  se mide mediante la pendiente de la recta tangente a la curva en dicho punto. A dicho valor se le llama derivada de
se mide mediante la pendiente de la recta tangente a la curva en dicho punto. A dicho valor se le llama derivada de  en el punto
en el punto  y se expresa
y se expresa 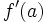 .
.
Ejercicios propuestos
|
Ejercicios propuestos: Crecimiento en un punto. Derivada |
Obtención de la derivada de una función en un punto
Hemos dicho que la derivada de una función  en un punto
en un punto  es la pendiente de la recta tangente a la curva en dicho punto, y se representa
es la pendiente de la recta tangente a la curva en dicho punto, y se representa 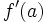 . Podemos obtener dicho valor mediante el concepto de límite:
. Podemos obtener dicho valor mediante el concepto de límite:
En esta escena podrás ver cómo se interpreta geométricamente el concepto de derivada de una función en un punto.
Ejemplos: Derivada de una función en un punto
Calcula la derivada de la función 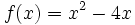 en el punto de abscisa
en el punto de abscisa 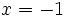
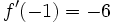
Aproximación intuitiva al concepto de función derivable.
Apróximación al concepto de derivada apoyándonos en la existencia o no de la recta tangente en un punto.
Definición rigurosa de derivada de una función en un punto.
Cálculo de derivada de 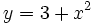 en el punto
en el punto 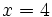 .
.
Cálculo de la derivada de 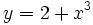 en el punto
en el punto 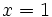 .
.
Cálculo de la derivada de 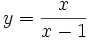 en el punto
en el punto  .
.
Cálculo de la derivada de 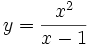 en el punto
en el punto  .
.
Cálculo de la derivada en un punto de una función a trozos.
Ejercicios propuestos
|
Ejercicios propuestos: Derivada de una función en un punto |