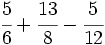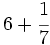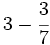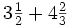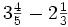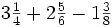Plantilla:Ejemplo suma fracciones
De Wikipedia
| Revisión de 16:44 18 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:57 18 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 93: | Línea 93: | ||
| |url1=https://www.youtube.com/watch?v=7eCKIMYzfCg | |url1=https://www.youtube.com/watch?v=7eCKIMYzfCg | ||
| }} | }} | ||
| - | {{Video_enlace_matefacil | + | {{Video_enlace |
| |titulo1=Ejemplo 7 | |titulo1=Ejemplo 7 | ||
| + | |duracion=8'24" | ||
| + | |sinopsis=Suma de fracciones (método del m.c.m.) | ||
| + | |||
| + | a) <math>\cfrac{3}{7}+ \cfrac{2}{7}</math> | ||
| + | |||
| + | b) <math>\cfrac{3}{4}+ \cfrac{5}{6}</math> | ||
| + | |||
| + | c) <math>\cfrac{1}{3}+ \cfrac{2}{9}+\cfrac{7}{18}</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=zi654ocYu98 | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejemplo 8 | ||
| + | |duracion=3'44" | ||
| + | |sinopsis=Resta de fracciones con distinto denominador (método del m.c.m.): | ||
| + | |||
| + | :<math>\cfrac{8}{5}- \cfrac{5}{4}</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=17AX9JcUJTw | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejemplo 9 | ||
| + | |duracion=6'46" | ||
| + | |sinopsis=Suma y resta de fracciones con distinto denominador (método del m.c.m.): | ||
| + | |||
| + | :<math>\cfrac{5}{4}- \cfrac{3}{8}+\cfrac{1}{3}</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=sr68FsJlUxQ | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejemplo 10 | ||
| |duracion=2'18" | |duracion=2'18" | ||
| |sinopsis=Suma y resta de fracciones con distinto denominador (método rápido): | |sinopsis=Suma y resta de fracciones con distinto denominador (método rápido): | ||
| Línea 103: | Línea 136: | ||
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejemplo 8 | + | |titulo1=Ejemplo 11 |
| |duracion=2'05" | |duracion=2'05" | ||
| |sinopsis=Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.): | |sinopsis=Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.): | ||
| Línea 114: | Línea 147: | ||
| ---- | ---- | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejemplo 9 | + | |titulo1=Ejemplo 12 |
| |duracion=0'48" | |duracion=0'48" | ||
| |sinopsis=Suma de un entero y una fracción: | |sinopsis=Suma de un entero y una fracción: | ||
| Línea 124: | Línea 157: | ||
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejemplo 10 | + | |titulo1=Ejemplo 13 |
| |duracion=0'43" | |duracion=0'43" | ||
| |sinopsis=Resta de un entero y una fracción. | |sinopsis=Resta de un entero y una fracción. | ||
| Línea 135: | Línea 168: | ||
| ---- | ---- | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejemplo 11 | + | |titulo1=Ejemplo 14 |
| |duracion=2'56" | |duracion=2'56" | ||
| |sinopsis=Suma de números mixtos. | |sinopsis=Suma de números mixtos. | ||
| Línea 145: | Línea 178: | ||
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejemplo 12 | + | |titulo1=Ejemplo 15 |
| |duracion=2'40" | |duracion=2'40" | ||
| |sinopsis=Resta de números mixtos. | |sinopsis=Resta de números mixtos. | ||
| Línea 155: | Línea 188: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 13 | + | |titulo1=Ejemplo 16 |
| |duracion=11'55" | |duracion=11'55" | ||
| |sinopsis=Suma y resta de números mixtos. | |sinopsis=Suma y resta de números mixtos. | ||
Revisión de 18:57 18 may 2017
Ejemplo: Suma y resta de fracciones
Calcula: 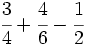
Solución:
Calculamos el m.c.m. de los denominadores:
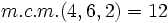
y reducimos las fracciones a común denominador:
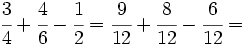
Una vez que tenemos las fracciones homogéneas, sumamos o restamos los númeradores, dejando el mismo denominador:
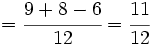
Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Otro método para sumar o restar fracciones, fácil de recordar, que no requiere del m.c.m, pero que a veces precisa simplificar más al final. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma y resta de fracciones con el mismo denominador:
a) 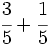 b)
b) 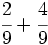 c)
c) 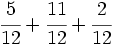 d)
d) 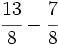 e)
e) 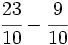
Suma y resta de fracciones con distinto denominador (método del m.c.m.):
a) 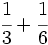 b)
b) 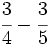
Suma de fracciones con distinto denominador (método rápido):
a) 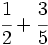
b) 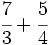
Resta de fracciones con distinto denominador (método rápido):
a) 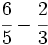
b) 
Suma de fracciones con distinto denominador (método del m.c.m.):
a) 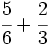 b)
b) 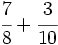 c)
c) 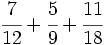
Suma y resta de fracciones con distinto denominador (método del m.c.m.):
Suma de fracciones (método del m.c.m.)
a) 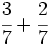
b) 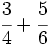
c) 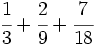
Resta de fracciones con distinto denominador (método del m.c.m.):
Suma y resta de fracciones con distinto denominador (método del m.c.m.):
Suma y resta de fracciones con distinto denominador (método rápido):
Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.):
Suma de un entero y una fracción:
Resta de un entero y una fracción.
Suma de números mixtos.
Resta de números mixtos.
Suma y resta de números mixtos.