Plantilla:Def fraccion
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:27 19 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:34 19 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja Amarilla|texto=Una '''fracción''' se expresa de la forma {{b}}<math>\cfrac {a}{b} \, ,</math>{{b}} con{{b}} <math>a,b \in \mathbb{Z}</math> <math>, \, b \ne 0</math>, donde <math>a\;\!</math> se llama '''numerador''' y <math>b\;\!</math> '''denominador'''. | + | {{Caja Amarilla|texto=Una '''fracción''' es es la expresión de una cantidad dividida entre otra cantidad; es decir que representa un cociente no efectuado de números. |
| - | *El '''denominador''' indica las partes iguales en que se divide la unidad. | + | |
| - | *El '''numerador''' indica las partes que tomamos de dicha división.}} | + | Se representa de la forma {{b}}<math>\cfrac {a}{b} \, ,</math>{{b}} con{{b}} <math>a,b \in \mathbb{Z}</math> <math>, \, b \ne 0</math>. También se puede representar <math>a/b\;</math>. |
| + | |||
| + | *El número <math>b\;\!</math> se llama '''denominador''' e indica las partes iguales en que se divide la unidad. | ||
| + | *El numero <math>a\;\!</math> se llama '''numerador''' e indica las partes que tomamos de dicha división.}} | ||
| {{p}} | {{p}} | ||
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
Revisión de 16:34 19 may 2017
Una fracción es es la expresión de una cantidad dividida entre otra cantidad; es decir que representa un cociente no efectuado de números.
Se representa de la forma 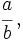 con
con 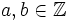
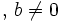 . También se puede representar
. También se puede representar 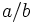 .
.
- El número
 se llama denominador e indica las partes iguales en que se divide la unidad.
se llama denominador e indica las partes iguales en que se divide la unidad.
- El numero
 se llama numerador e indica las partes que tomamos de dicha división.
se llama numerador e indica las partes que tomamos de dicha división.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según el valor las fracciones pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.

