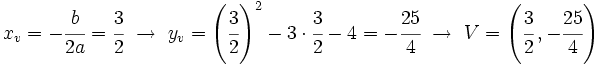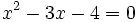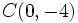Funciones Cuadráticas. Parábolas (4ºESO Académicas)
De Wikipedia
| Revisión de 17:24 19 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:33 19 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | ==Función cuadrática== | ||
| + | {{definición de funcion cuadratica}} | ||
| + | {{p}} | ||
| + | |||
| + | ==Representación gráfica de la función cuadrática== | ||
| + | Vamos a empezar con un ejemplo sencillo que nos permita una primera aproximación a la representación gráfica de este tipo de funciones: | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo: ''La función cuadrática tipo''|enunciado= | ||
| + | Representa la función cuadrática más sencilla de todas, la llamada '''función cuadrática tipo''', cuya ecuación es: | ||
| + | |||
| + | <center><math>y=x^2\;</math></center> | ||
| + | |||
| + | |sol= | ||
| + | {{Tabla75|celda2=[[Imagen:graf_x_2.png|center|350px]] | ||
| + | |celda1= | ||
| + | |||
| + | Haremos una tabla de valores y, a partir de ella, dibujaremos su gráfica: | ||
| + | |||
| + | [[Imagen:tabla_x_2.png|center]] | ||
| + | |||
| + | Los valores de esta tabla los representamos en unos ejes cartesianos a una escala adecuada. (Son los puntos rojos de la imagen de la derecha). | ||
| + | |||
| + | La gráfica obtenida recibe el nombre de '''parábola'''. | ||
| + | |||
| + | *Fíjate como su gráfica es simétrica. | ||
| + | |||
| + | *El '''eje''' de simetría (en verde) divide a la parábola en dos '''ramas''' simétricas. | ||
| + | |||
| + | *El eje corta a la parábola en un punto llamado '''vértice''' (V en el dibujo). | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | La gráfica de cualquier otra función cuadrática tiene un aspecto muy parecido al de la "función cuadrática tipo" que acabamos de representar. | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| + | La representación gráfica de la función cuadrática recibe el nombre de '''parábola''' y tiene las siguientes propiedades: | ||
| + | *La parábola es simétrica respecto de un eje paralelo al eje Y, que llamaremos '''eje''' de la parábola. | ||
| + | *El eje de la parábola corta a la parábola por un punto llamado '''vértice'''. La abscisa del vértice es <math>x=-\cfrac{b}{2a}</math>. | ||
| + | *El eje de la parábola la divide en dos partes denominadas '''ramas'''. | ||
| + | **Si <math>a>0\;</math>, la parábola tiene las ramas hacia arriba. | ||
| + | **Si <math>a<0\;</math>, la parábola tiene las ramas hacia abajo. | ||
| + | *Cuanto mayor es <math>|a|\;</math>, más estilizada es la parábola. | ||
| + | *Dos parábolas con el mismo coeficiente <math>a\;</math>, tienen formas idénticas aunque están situadas en posiciones distintas. | ||
| + | *'''Puntos de corte con los ejes''': | ||
| + | **Eje Y: En el punto <math>(0,c)\;</math> | ||
| + | **Eje X: En los puntos (x,0), donde x se obtiene resolviendo la ecuación <math>ax^2+bx+c=0\;</math>. Pueden ser 0,1 ó 2 puntos. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo: ''Representación gráfica de la función cuadrática''|enunciado=Representa <math>y = x^2-3x-4\;</math>. | ||
| + | |sol= | ||
| + | *'''Vértice:''' | ||
| + | :<math>x_v=-\cfrac{b}{2a}=\cfrac{3}{2} \ \rightarrow \ y_v=\left( \cfrac{3}{2} \right )^2-3 \cdot \cfrac{3}{2} -4 = -\cfrac{25}{4} \ \rightarrow \ V=\left( \cfrac{3}{2} \, ,-\cfrac{25}{4} \right )</math> | ||
| + | |||
| + | *'''Puntos de corte con los ejes:''' | ||
| + | |||
| + | :Eje X: Resolvemos la ecuación: <math>x^2-3x-4=0\;</math> | ||
| + | {{p}} | ||
| + | :<math>x=\cfrac{3 \pm \sqrt{9+16}}{2} \ \rightarrow \ \left\{ \begin{matrix} x_1=-1 \ \rightarrow \ A(-1,0) \\ x_2=~4 \quad \rightarrow \ \ B(4,0) \end{matrix} \right.</math> | ||
| + | |||
| + | :Eje Y: <math>C(0,-4)\;</math> | ||
| + | |||
| + | *'''Tabla de valores:''' | ||
| + | |||
| + | [[Imagen:tabla_fcuad.png|center]] | ||
| + | |||
| + | *'''Gráfica:''' | ||
| + | |||
| + | [[Imagen:grafica_fcuad.png|center|350px]] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=La función cuadrática|enunciado= | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=Funciones cuadráticas básicas | |titulo1=Funciones cuadráticas básicas | ||
| Línea 16: | Línea 87: | ||
| |sinopsis=:Las parábolas. Puntos de corte con los ejes y ramas. | |sinopsis=:Las parábolas. Puntos de corte con los ejes y ramas. | ||
| |url1=https://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/27-las-parabolas-3 | |url1=https://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/27-las-parabolas-3 | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 1 | ||
| + | |duracion=15'45" | ||
| + | |sinopsis=Representa gráficamente la función <math>y=x^2+8x+15\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=E6ysFJEIyEc | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 2 | ||
| + | |duracion=8'46" | ||
| + | |sinopsis=Representa gráficamente la función <math>y=2x-x^2\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=0pUnHF1FJ2s | ||
| }} | }} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Ejemplo 3 |
| - | |duracion=3'13" | + | |duracion=7'02" |
| - | |sinopsis=Representa: <math>y= x^2-5x+6\;</math> | + | |sinopsis=Representa gráficamente la función <math>y=x^2-5x+6\;</math> |
| - | |url1=https://www.youtube.com/watch?v=EVTfYEUOHP4 | + | |url1=http://www.unicoos.com/video/matematicas/3-eso/funciones-y-graficas/funciones-de-segundo-grado/representacion-funcion-cuadratica |
| }} | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicios 2 | ||
| - | |duracion=7'07" | ||
| - | |sinopsis=:Cálculo de la parábola que pasa por tres o cuatro puntos. | ||
| - | |url1=https://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/2701-ejercicio-5 | ||
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | {{p}} |
| - | |titulo1=Tasa de variación de una parábola | + | {{Geogebra_enlace |
| - | |duracion=7'57" | + | |descripcion=Escena en la que podrás ver como afecta a la gráfica de la función cuadrática modificar los coeficientes de la ecuación. |
| - | |sinopsis=:Tasa de variación de una función cuadrática. | + | |enlace=[https://ggbm.at/rjsG4Vmq Función cuadrática] |
| - | |url1=https://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/28-tasa-de-cambio-de-una-parabola-3 | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Escena en la que podrás ver la representación gráfica de la función cuadrática y calcular su vértice y puntos de corte con los ejes. | ||
| + | |enlace=[https://ggbm.at/D4VgFKRW Función cuadrática: vértice y puntos de corte con los ejes] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Función cuadrática|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Función cuadrática'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | Dada la función <math>y=x^2-3x-4\;</math>: | ||
| + | |||
| + | :a) Halla su vértice. | ||
| + | :b) Halla los puntos de corte con los ejes. | ||
| + | :c) Haz una tabla de valores para valores de x comprendidos entre -2 y 5. | ||
| + | :d) Representala para valores de x comprendidos entre -5 y 5. | ||
| + | |||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=extrema x^2-3x-4}} | ||
| + | :b) {{consulta|texto=intercept x^2-3x-4}} | ||
| + | :c) {{consulta|texto=Table[x^2-3x-4,{x,-2,5,1}]}} | ||
| + | :d) {{consulta|texto=plot x^2-3x-4, x=-5 to 5}} | ||
| + | |||
| + | |||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión de 17:33 19 may 2017
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Función cuadrática
Una función cuadrática es aquella cuya expresión analítica puede escribirse como una ecuación polinómica de segundo grado:
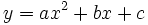 |
con 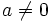 .
.
Representación gráfica de la función cuadrática
Vamos a empezar con un ejemplo sencillo que nos permita una primera aproximación a la representación gráfica de este tipo de funciones:
Ejemplo: La función cuadrática tipo
Representa la función cuadrática más sencilla de todas, la llamada función cuadrática tipo, cuya ecuación es:
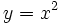
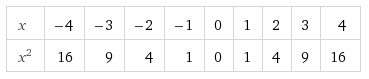
| Haremos una tabla de valores y, a partir de ella, dibujaremos su gráfica:
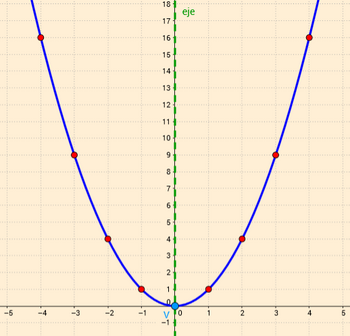
Los valores de esta tabla los representamos en unos ejes cartesianos a una escala adecuada. (Son los puntos rojos de la imagen de la derecha). La gráfica obtenida recibe el nombre de parábola.
|
La gráfica de cualquier otra función cuadrática tiene un aspecto muy parecido al de la "función cuadrática tipo" que acabamos de representar.
Propiedades
La representación gráfica de la función cuadrática recibe el nombre de parábola y tiene las siguientes propiedades:
- La parábola es simétrica respecto de un eje paralelo al eje Y, que llamaremos eje de la parábola.
- El eje de la parábola corta a la parábola por un punto llamado vértice. La abscisa del vértice es
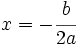 .
.
- El eje de la parábola la divide en dos partes denominadas ramas.
- Si
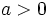 , la parábola tiene las ramas hacia arriba.
, la parábola tiene las ramas hacia arriba.
- Si
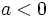 , la parábola tiene las ramas hacia abajo.
, la parábola tiene las ramas hacia abajo.
- Si
- Cuanto mayor es
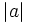 , más estilizada es la parábola.
, más estilizada es la parábola.
- Dos parábolas con el mismo coeficiente
 , tienen formas idénticas aunque están situadas en posiciones distintas.
, tienen formas idénticas aunque están situadas en posiciones distintas.
- Puntos de corte con los ejes:
- Eje Y: En el punto
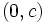
- Eje X: En los puntos (x,0), donde x se obtiene resolviendo la ecuación
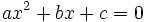 . Pueden ser 0,1 ó 2 puntos.
. Pueden ser 0,1 ó 2 puntos.
- Eje Y: En el punto
Ejemplo: Representación gráfica de la función cuadrática
Representa 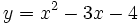 .
.
Representación gráfica de las funciones cuadráticas 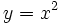 e
e 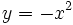 .
.
- Las parábolas. Puntos de corte con los ejes y ramas.
Representa gráficamente la función 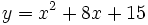
Representa gráficamente la función 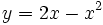
Representa gráficamente la función 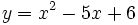
Escena en la que podrás ver como afecta a la gráfica de la función cuadrática modificar los coeficientes de la ecuación.
Escena en la que podrás ver la representación gráfica de la función cuadrática y calcular su vértice y puntos de corte con los ejes.
|
Actividad: Función cuadrática Dada la función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|