Plantilla:Razones trigonométricas de un ángulo cualquiera
De Wikipedia
| Revisión de 10:19 24 may 2017 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) ← Ir a diferencia anterior |
Revisión de 10:28 24 may 2017 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| |duracion=7´26" | |duracion=7´26" | ||
| |url1=https://www.youtube.com/watch?v=sUcQakSvKFk | |url1=https://www.youtube.com/watch?v=sUcQakSvKFk | ||
| - | |sinopsis=Interpretación geométrica del seno usando la circunferencia goniométrica y análisis de sus signo y crecimiento o decrecimiento según los cuadfrantes | + | |sinopsis=Interpretación geométrica del seno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. |
| + | |||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| Línea 51: | Línea 52: | ||
| |duracion=7´54" | |duracion=7´54" | ||
| |url1=https://www.youtube.com/watch?v=OPV_mEjYGiU | |url1=https://www.youtube.com/watch?v=OPV_mEjYGiU | ||
| - | |sinopsis=Interpretación geométrica del coseno usando la circunferencia goniométrica y análisis de sus signo y crecimiento o decrecimiento según los cuadfrantes | + | |sinopsis=Interpretación geométrica del coseno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. |
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| Línea 57: | Línea 58: | ||
| |duracion=7´41" | |duracion=7´41" | ||
| |url1=https://www.youtube.com/watch?v=6iTdq2vNwd0 | |url1=https://www.youtube.com/watch?v=6iTdq2vNwd0 | ||
| - | |sinopsis=Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de sus signo y crecimiento o decrecimiento según los cuadfrantes | + | |sinopsis=Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. |
| + | |||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=La cosecante en la circunferencia goniométrica | ||
| + | |duracion=15´21" | ||
| + | |url1=https://www.youtube.com/watch?v=VjduOmeRh8o | ||
| + | |sinopsis=Interpretación geométrica de la cosecante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=La secante en la circunferencia goniométrica | ||
| + | |duracion=13´06" | ||
| + | |url1=https://www.youtube.com/watch?v=MAMtOCJvIl8 | ||
| + | |sinopsis=Interpretación geométrica de la secante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=La cotangente en la circunferencia goniométrica | ||
| + | |duracion=13´30" | ||
| + | |url1=https://www.youtube.com/watch?v=u0O34kVmqPE | ||
| + | |sinopsis=Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
Revisión de 10:28 24 may 2017
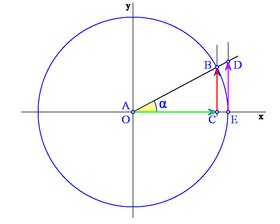
Obsérvese como, en el apartado anterior, las coordenadas del punto B son 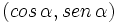 . Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
. Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
- Dado un ángulo
 , se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del lado terminal del ángulo con la circunferencia goniométrica:
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del lado terminal del ángulo con la circunferencia goniométrica:
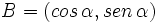
- Definiremos la tangente del ángulo, como:
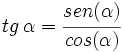 ,
, 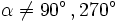
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
Signo de las razones trigonométricas
Determinación del signo de las razones trigonométricas
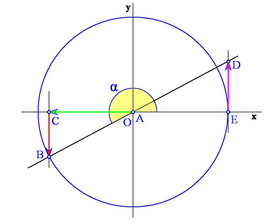
- Signo del coseno: Según en qué cuadrante esté el ángulo, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, el signo del coseno será positivo si está a la derecha de O y negativo si está a la izquierda.
- Signo del seno: Según el cuadrante en el que esté el ángulo, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Así el signo del seno será positivo si está por encima y negativo si está por debajo.
En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante.
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
Si el lado origen de un ángulo orientado es el semieje OX, del cuadrante en que está el lado extremo se dice "cuadrante del ángulo". En este video definimos las razones trigonométricas de un ángulo orientado, y para ello empleamos las coordenadas de un punto cualquiera (a;b) del lado extremo.
Interpretación geométrica del seno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica del coseno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la cosecante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la secante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
3 ejercicios sobre razones trigonométricas de ángulos orientados.