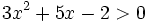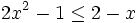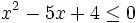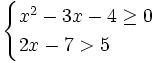Plantilla:Inecuaciones cuadráticas con una incógnita
De Wikipedia
| Revisión de 10:02 28 may 2017 Coordinador (Discusión | contribuciones) (→Resolución de inecuaciones cuadráticas con una incógnita) ← Ir a diferencia anterior |
Revisión de 10:06 28 may 2017 Coordinador (Discusión | contribuciones) (→Resolución de inecuaciones cuadráticas con una incógnita) Ir a siguiente diferencia → |
||
| Línea 102: | Línea 102: | ||
| |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo por intervalos. | |sinopsis=Resuelve: <math>x^2+5x-2 \le x-2\;</math> analizando el signo por intervalos. | ||
| |url1=https://www.youtube.com/watch?v=QUkdNCE5_mw&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=37 | |url1=https://www.youtube.com/watch?v=QUkdNCE5_mw&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=37 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=7'44" | ||
| + | |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo de los factores. | ||
| + | |url1=https://www.youtube.com/watch?v=sq98v0gHvLg&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=38 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=7'22" | ||
| + | |sinopsis=Resuelve: <math>x^2 < 9\;</math> analizando el signo por intervalos. | ||
| + | |url1=https://www.youtube.com/watch?v=vCFX0G8YJuo&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=39 | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 10:06 28 may 2017
Una inecuación cuadrática con una incógnita es una inecuación en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de segundo grado en una sola variable. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
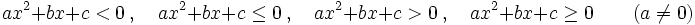
Resolución de inecuaciones cuadráticas con una incógnita
Para resolver estas inecuaciones usaremos el método gráfico. Este método requiere que el miembro de la derecha de la inecuación sea cero, lo cual siempre se puede conseguir mediante transformaciones.
En la escena vamos a resolver la siguiente inecuación:
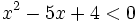
Representamos la parábola 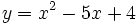 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
En realidad basta hallar los puntos de corte con el eje X y determinar la dirección de las ramas a partir del signo del coeficiente de 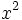 .
.
En este caso, los puntos de corte son 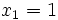 y
y 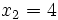 , soluciones de la ecuación de segundo grado
, soluciones de la ecuación de segundo grado
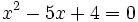
y las ramas va hacia arriba porque el coeficiente de 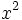 es positivo.
es positivo.
Resuelve:
- a)
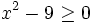
- b)
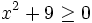
- c)
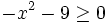
- d)
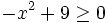
Resuelve: 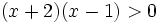 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 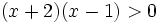 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 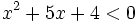 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 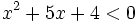 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 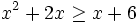 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 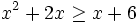 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 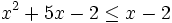 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 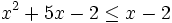 analizando el signo por intervalos.
analizando el signo por intervalos.
Resuelve: 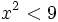 analizando el signo de los factores.
analizando el signo de los factores.
Resuelve: 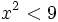 analizando el signo por intervalos.
analizando el signo por intervalos.
Resolución de sistemas de inecuaciones cuadráticas con una incógnita
Para resolver un sistema de inecuaciones cuadráticas con una incógnita, hay que resolver cada inecuación por separado y finalmente seleccionar la solución común a ambas (intersección de los conjuntos solución de ambas).