Operaciones con potencias (1ºESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 06:56 30 may 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las potencias de números naturales) ← Ir a diferencia anterior |
Revisión de 19:10 31 may 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las potencias de números naturales) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| {{propiedades potencias naturales}} | {{propiedades potencias naturales}} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | + | {{Ejemplo: propiedades potencias naturales}} |
| - | *'''Producto de potencias de la misma base:''' | + | |
| - | {{p}} | ||
| - | <center><math>\begin{matrix} 5^4 \cdot 5^3 \, \\ \; \end{matrix} | ||
| - | \begin{matrix} \ = \ \\ \; \end{matrix} | ||
| - | \begin{matrix} \underbrace{ (5 \cdot 5 \cdot 5 \cdot 5) } \\ 4 \, \mbox{veces} \end{matrix} | ||
| - | \begin{matrix} \ \cdot \ \\ \; \end{matrix} | ||
| - | \begin{matrix} \underbrace{ (5 \cdot 5 \cdot 5) } \\ 3 \, \mbox{veces} \end{matrix} | ||
| - | \begin{matrix} \ = \ \\ \; \end{matrix} | ||
| - | \begin{matrix} 5^{4+3} = 5^7 \\ \; \end{matrix} | ||
| - | </math> | ||
| - | |||
| - | </center> | ||
| - | <br> | ||
| - | *'''Potencia de un producto:''' | ||
| - | <center><math>(2 \cdot 3)^3 = 6^3 = 6 \cdot 6 \cdot 6 = 216</math></center> | ||
| - | {{p}} | ||
| - | <center><math>2^3 \cdot 3^3 = (2 \cdot 2 \cdot 2) \cdot (3 \cdot 3 \cdot 3) = 8 \cdot 27 = 216</math></center> | ||
| - | {{p}} | ||
| - | <center>Las dos formas de hacerlo son equivalentes.</center> | ||
| - | <br> | ||
| - | *'''Potencia de un cociente:''' | ||
| - | <center><math>(6 : 3)^3 = 2^3 = 2 \cdot 2 \cdot 2 = 8</math></center> | ||
| - | {{p}} | ||
| - | <center><math>6^3 : 2^3 = 16 : 27 = 8\;</math></center> | ||
| - | {{p}} | ||
| - | <center>Las dos formas de hacerlo son equivalentes.</center> | ||
| - | <br> | ||
| - | *'''Potencia de otra potencia:''' | ||
| - | {{p}} | ||
| - | <center><math>(5^4)^3 = 5^4 \cdot 5^4 \cdot 5^4 = 5^{4+4+4} = 5^{4 \cdot 3} = 5^{12}</math></center> | ||
| - | <br> | ||
| - | *'''Potencia cero:''' Cuando se vio la definición de potencia, dijimos que {{sube|porcentaje=15%|contenido=<math>a^0 = 1\;</math>}} por convenio. Expliquemos ésto ahora un poco mejor: | ||
| - | <center> | ||
| - | <math>\left.\begin{matrix} | ||
| - | 5^3:5^3 =5^{3-3}=5^0 | ||
| - | \\ | ||
| - | 5^3:5^3=125:125=1 | ||
| - | |||
| - | \end{matrix}\right\} \ \rightarrow \ 5^0 = 1</math> | ||
| - | </center> | ||
| - | |||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Propiedades de las operaciones con potencias|enunciado= | {{Videotutoriales|titulo=Propiedades de las operaciones con potencias|enunciado= | ||
Revisión de 19:10 31 may 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 31)
Propiedades de las potencias de números naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
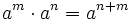
- 2. Cociente de potencias de la misma base:
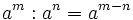
- 3. Potencia de un producto:
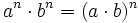
- 4. Potencia de un cociente:
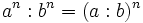
- 5. Potencia de otra potencia:
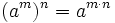
- Producto de potencias de la misma base:
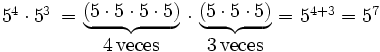
- Cociente de potencias de la misma base:
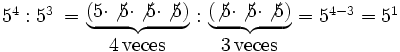
- Potencia de un producto:
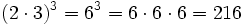
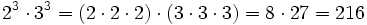
Las dos formas de hacerlo son equivalentes.
- Potencia de un cociente:
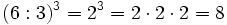
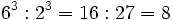
Las dos formas de hacerlo son equivalentes.
- Potencia de otra potencia:
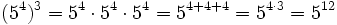
- Potencia cero: Cuando se vio la definición de potencia, dijimos que
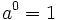 por convenio. Expliquemos ésto ahora un poco mejor:
por convenio. Expliquemos ésto ahora un poco mejor:
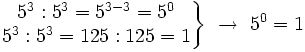
Propiedades de las potencias y ejemplos:
- Potencias de exponente 0.
- Potencias de exponente 1.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
Propiedades de las potencias y ejemplos:
- Potencia de otra potencia.
- Potencia de un producto.
- Potencia de un cociente.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
- Potencia de otra potencia.
- Ejemplos.
Aprende a multiplicar potencias con la misma base
Aprende a dividir potencias con la misma base
Aprende a calcular la potencia de otra potencia
(Pág. 31-32)
Ejercicios resueltos: Operaciones con potencias
- a) Calcula por el camino más sencillo:
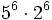
- b) Calcula por el camino más sencillo:
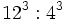
- c) Calcula con la ayuda de las propiedades:
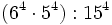
- d) Calcula con la ayuda de las propiedades:
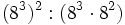
- e) Reduce a una sola potencia:
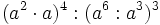
Solución:
- a) Aplicando la propiedad 3:
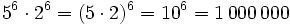
- b) Aplicando la propiedad 4:
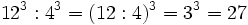
- c) Aplicando la propiedad 3:
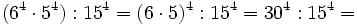
- y aplicando la propiedad 4:
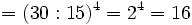
- d) Aplicando las propiedades 5 y 1:
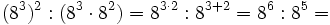
- y aplicando la propiedad 2:
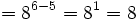
- e) Por las propiedades 1 y 2:
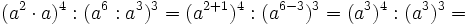
- y por las propiedades 5 y 2:
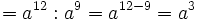
Ejercicios propuestos
|
Ejercicios propuestos: Operaciones con potencias |

