Plantilla:Transformaciones elementales de funciones (1ºBach)
De Wikipedia
| Revisión de 18:03 21 may 2017 Coordinador (Discusión | contribuciones) (→Dilatación y contracción) ← Ir a diferencia anterior |
Revisión de 11:38 4 jun 2017 Coordinador (Discusión | contribuciones) (→Actividades) Ir a siguiente diferencia → |
||
| Línea 137: | Línea 137: | ||
| |url1=https://www.youtube.com/watch?v=CTRR0d56ePo | |url1=https://www.youtube.com/watch?v=CTRR0d56ePo | ||
| }} | }} | ||
| - | + | ---- | |
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Transformaciones de parábolas | ||
| + | |duracion=15'48" | ||
| + | |sinopsis=Tutorial en el que se explica como representar funciones del tipo f(x)=ax^2+bx+c utilizando la traslación de ejes. | ||
| + | |url1=https://www.youtube.com/watch?v=8yWFs-DYurk&list=PLZNmE9BEzVIk3VQdqC9kJ8pcR0iJJMh87&index=4 | ||
| + | }} | ||
| }} | }} | ||
Revisión de 11:38 4 jun 2017
Tabla de contenidos |
Traslación vertical y horizontal
- Traslación vertical: Sea
 una función y
una función y 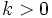 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 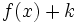 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia arriba y la de
unidades hacia arriba y la de 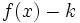 desplazándola
desplazándola  unidades hacia abajo.
unidades hacia abajo.
- Traslación horizontal: Sea
 una función y
una función y 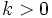 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 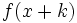 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia la izquierda y la de
unidades hacia la izquierda y la de 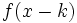 desplazándola
desplazándola  unidades hacia la derecha.
unidades hacia la derecha.
En esta escena podrás ver la representación conjunta una función y su transformada por traslación horizontal o vertical.
Simetrías
- Simetría respecto del eje X: Las gráficas de las funciones
 y
y 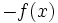 son simétricas respecto del eje de abscisas.
son simétricas respecto del eje de abscisas.
- Simetría respecto del eje Y: Las gráficas de las funciones
 y
y 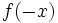 son simétricas respecto del eje de ordenadas.
son simétricas respecto del eje de ordenadas.
- Simetría respecto del origen: Las gráficas de las funciones
 y
y 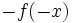 son simétricas respecto del origen de coordenadas.
son simétricas respecto del origen de coordenadas.
En esta escena podrás ver la representación conjunta una función y su simétrica.
La función "f" se dice "par" si f(-x) = f(x), y se dice "impar" si f(-x) = -f(x). Si "f" es par, su gráfica es simétrica respecto al eje de ordenadas. Si "f" es impar, su gráfica es simétrica respecto al origen de coordenadas. Obvio: si Dom f. no es simétrico respecto al punto "0", la función "f" no es par ni impar.
Dilatación y contracción
Vertical:
- Si
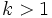 , la gráfica de la función
, la gráfica de la función 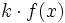 es una dilatación vertical de la gráfica de
es una dilatación vertical de la gráfica de  .
.
- Si
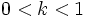 , la gráfica de la función
, la gráfica de la función 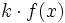 es una contracción vertical vertical de la gráfica de
es una contracción vertical vertical de la gráfica de  .
.
Horizontal:
- Si
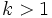 , la gráfica de la función
, la gráfica de la función 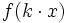 es una contracción horizontal de la gráfica de
es una contracción horizontal de la gráfica de  .
.
- Si
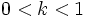 , la gráfica de la función
, la gráfica de la función 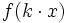 es una dilatación horizontal de la gráfica de
es una dilatación horizontal de la gráfica de  .
.
En esta escena podrás ver la representación conjunta una función y su transformada por dilatación o contracción.
Representa las funciones:
1) 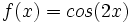
2) 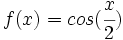
Representa las funciones:
1) 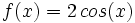
2) 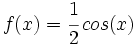
Representa las funciones:
1) 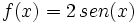
2) 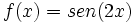
2) 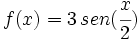
Actividades
En esta escena podrás practicar las transformaciones de funciones. Se te propondrán algunos ejercicios.
Representa 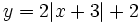 a partir de la gráfica de
a partir de la gráfica de 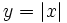
Determina la ecuación de una función tipo valor absoluto a partir de su gráfica, describiendo las transformaciones sufridas a partir de la gráfica de 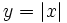 .
.
Halla la ecuación de la función que resulta de reflejar sobre el eje X y comprimir verticalmente en un factor de 8/3, la función 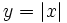 .
.
Representa la función: 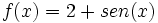 .
.
Representa la función: 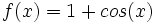 .
.
Representa la función: 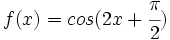 .
.
Representa la función: 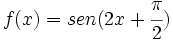 .
.
Tutorial en el que se explica como representar funciones del tipo f(x)=ax^2+bx+c utilizando la traslación de ejes.

