Plantilla:Raíces: definición y propiedades
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:49 1 jun 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las raíces) ← Ir a diferencia anterior |
Revisión de 08:36 10 jun 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las raíces) Ir a siguiente diferencia → |
||
| Línea 35: | Línea 35: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Raíz n-ésmina de un número|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=9´53" | ||
| + | |sinopsis=Tutorial que explica la definición de raíz (radical) realizando el cálculo de alguna raíces exactas de números racionales (enteros y decimales). | ||
| + | |url1=https://www.youtube.com/watch?v=OGeUwOWowGQ&index=1&list=PLZNmE9BEzVImIKACrwlnJVOz_w7oxAoRy | ||
| + | }} | ||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| - | |titulo1=Raíz n-ésmina de un número (parte I) | + | |titulo1=Tutorial 2 (parte I) |
| |duracion=6´38" | |duracion=6´38" | ||
| |sinopsis=Raíz n-ésmina de un número. Ejemplos sencillos. | |sinopsis=Raíz n-ésmina de un número. Ejemplos sencillos. | ||
| Línea 42: | Línea 49: | ||
| }} | }} | ||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| - | |titulo1=Raíz n-ésmina de un número (parte II) | + | |titulo1=Tutorial 2 (parte II) |
| |duracion=6´38" | |duracion=6´38" | ||
| |sinopsis=Raíz n-ésmina de un número. Ejemplos más complejos. | |sinopsis=Raíz n-ésmina de un número. Ejemplos más complejos. | ||
| |url1=https://www.youtube.com/watch?v=_b8Vha5epFU&index=6&list=PLWRbPOo5oaTf_vLErckNhkqH29aE696DA | |url1=https://www.youtube.com/watch?v=_b8Vha5epFU&index=6&list=PLWRbPOo5oaTf_vLErckNhkqH29aE696DA | ||
| + | }} | ||
| }} | }} | ||
Revisión de 08:36 10 jun 2017
Raíz n-ésima de un número
La raíz n-ésima  de un número
de un número 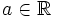 es otro número
es otro número 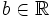 tal que
tal que 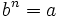 y que escribimos simbólicamente
y que escribimos simbólicamente ![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png) .
.
![\sqrt[n]{a}=b \iff b^n =a](/wikipedia/images/math/f/f/7/ff79017c635440f207b67b250c3660fb.png)
El número  se llama radicando, el número
se llama radicando, el número  índice y
índice y  la raíz.
la raíz.
Propiedades de las raíces
Propiedades
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) ;
; ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
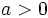 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
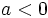 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 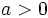 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
- Si el índice
 es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
Tutorial que explica la definición de raíz (radical) realizando el cálculo de alguna raíces exactas de números racionales (enteros y decimales).
Raíz n-ésmina de un número. Ejemplos sencillos.
Raíz n-ésmina de un número. Ejemplos más complejos.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 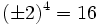 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 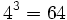 .
.
![\sqrt[3]{-8}=-2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png) porque
porque 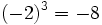 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).

