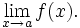Límite de una función (2ºBach)
De Wikipedia
| Revisión de 12:16 22 jun 2017 Coordinador (Discusión | contribuciones) (→Definición formal de límite) ← Ir a diferencia anterior |
Revisión de 12:20 22 jun 2017 Coordinador (Discusión | contribuciones) (→Funciones sin límite en un punto) Ir a siguiente diferencia → |
||
| Línea 100: | Línea 100: | ||
| :<math> | :<math> | ||
| D(x) = \begin{cases} | D(x) = \begin{cases} | ||
| - | c & \mathrm{para \ } x \ \mathrm{racional} \\ | + | c & \mathrm{si \ } x \, \in \mathbb{Q} \\ |
| - | d & \mathrm{para \ } x \ \mathrm{irracional} \\ | + | d & \mathrm{si \ } x \, \in \mathbb{I} \\ |
| \end{cases}</math> | \end{cases}</math> | ||
| no tiene ningún número <math>a\;</math> en el dominio para el cual exista el <math>\lim_{x \to a}f(x).</math> | no tiene ningún número <math>a\;</math> en el dominio para el cual exista el <math>\lim_{x \to a}f(x).</math> | ||
| - | |sol=Para demostrar la anterior afirmación, es necesario hacer uso del hecho de que cada intervalo contiene tanto números racionales como irracionales. | + | |sol=Para demostrar la anterior afirmación, es necesario hacer uso del hecho de que cualquier intervalo contiene tanto números racionales como irracionales. |
| }} | }} | ||
| Línea 115: | Línea 115: | ||
| |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/09-funciones-sin-limite-en-un-punto | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/09-funciones-sin-limite-en-un-punto | ||
| }} | }} | ||
| - | |||
| - | |||
| ==Límites laterales== | ==Límites laterales== | ||
Revisión de 12:20 22 jun 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Límite de de una función en un punto
El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
La clave para entender el Cálculo Diferencial de una variable y divertirse con él es aprender a "meterse en la piel" de un habitante genérico "x" de la recta real. En este vídeo describimos la vida de "x" ("x" eres tú) en el alambre infinito donde vive: un universo de una única dimensión.
- Los puntos en la recta real.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
- Concepto de distancia entre dos puntos.
- Concepto de entorno de un punto.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
 y
y  .
.
En este vídeo, el más importante de todos, hablamos del mágico instante en que tú, el número real "x", por amor, consagras gozosamente tu existencia a la observación y análisis de la Dulcinea "f(x)" que da sentido a tu vida y la llena de alegría y diversión.
Definición informal de límite
De manera informal, diremos que una función 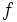 tiene límite
tiene límite 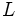 en
en 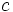 , o que
, o que 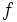 tiende a
tiende a 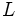 cuando
cuando 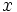 se acerca a
se acerca a 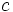 , si se puede hacer que
, si se puede hacer que 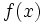 esté tan cerca como queramos de
esté tan cerca como queramos de 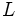 , haciendo que
, haciendo que 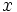 esté suficientemente cerca de
esté suficientemente cerca de 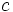 , pero sin llegar a
, pero sin llegar a 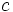 .
.
Definición formal de límite
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función  , cuando
, cuando 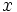 tiende a
tiende a 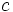 , es
, es 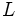 , si y sólo si, para todo
, si y sólo si, para todo 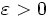 , existe un
, existe un 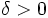 , tal que para todo número real
, tal que para todo número real 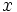 del dominio de la función, si
del dominio de la función, si 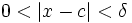 , entonces
, entonces 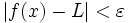 .
.
En notación formal:
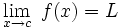
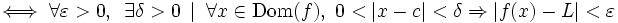
Esta es una formulación estricta del concepto de límite de una función real en un punto de acumulación del dominio de la función y se debe al matemático francés Luis Cauchy.
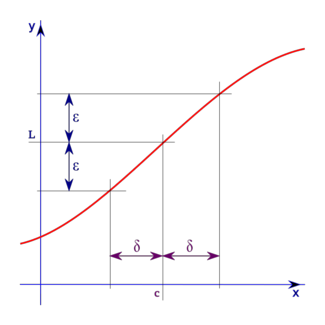
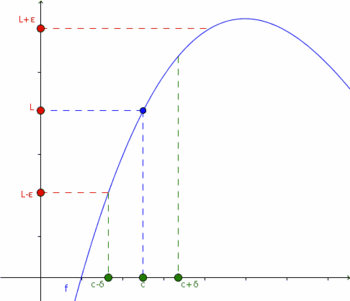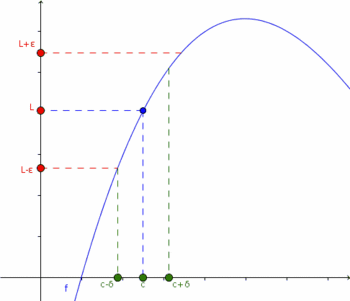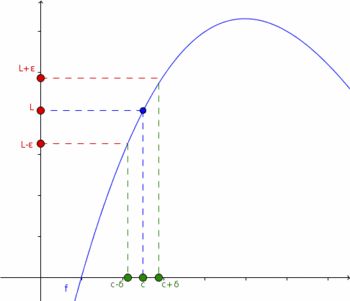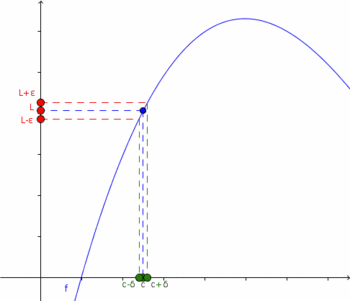
Definición rigurosa de límite de una función en un punto.
Límite de una función en un punto
Demostrar que 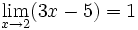 usando la definición formal de límite.
usando la definición formal de límite.
Utilizando la definición, debemos demostrar que para cualquier 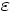 dado podemos hallar un
dado podemos hallar un 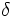 para el cual se cumpla:
para el cual se cumpla:
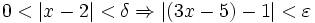 [1]
[1]Tomando 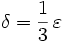 será posible probar esto. Esto es válido ya que nos permite obtener un valor para cualquier
será posible probar esto. Esto es válido ya que nos permite obtener un valor para cualquier 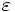 dado, que es precisamente lo que enuncia la definición.
dado, que es precisamente lo que enuncia la definición.
Probaremos entonces la tesis, tomando como hipótesis:
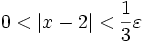 [2]
[2]Dado que
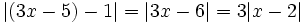
y que , por [2]:
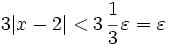
queda demostrado [1].
Nótese que bien podríamos haber elegido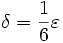 o
o 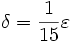 , por ejemplo. En tanto
, por ejemplo. En tanto 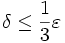 , siempre podremos demostrar [1].
, siempre podremos demostrar [1].Funciones sin límite en un punto
Función sin límite
Para demostrar la anterior afirmación, es necesario hacer uso del hecho de que cualquier intervalo contiene tanto números racionales como irracionales.
Sólo tiene sentido calcular los límites laterales de una función en un punto cuando la función está definida en las "proximidades" del punto.
Límites laterales
En este vídeo hablamos de los dos límites laterales de una función "f" en un punto "a" (límite de "f" en "a" por la izquierda y límite de "f" en "a" por la derecha), interpretándolos en términos geométricos. Si dichos dos límites laterales de "f" en "a" son iguales a "L", se dice que "L" es el límite de "f" en "a".
- Conceptos de límite de una función por la derecha y por la izquierda de un punto.
- Concepto de límite de una función en un punto.
- Se puede calcular el límite en un punto independientemente de que el punto pertenezca o no al dominio de la función. Ejemplos.
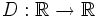 definida como:
definida como:
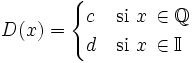
 en el dominio para el cual exista el
en el dominio para el cual exista el