Plantilla:Relación entre ángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:58 4 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:33 5 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| |descripcion=En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice. | |descripcion=En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice. | ||
| |enlace=[https://ggbm.at/WSw5AKar Ángulos complementarios, suplementarios y opuestos por el vértice] | |enlace=[https://ggbm.at/WSw5AKar Ángulos complementarios, suplementarios y opuestos por el vértice] | ||
| + | }} | ||
| + | {{AI_anaya | ||
| + | |titulo1=Autoevaluación: ''Relaciones entre ángulos'' | ||
| + | |descripcion= | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/02.htm | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/02.htm | ||
| }} | }} | ||
Revisión de 15:33 5 jul 2017
|  Ángulos consecutivos
 |
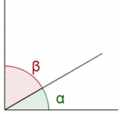
Relaciones entre ángulos (4´36") Sinopsis: Con este video vamos a estudiar la clasificación de los ángulos de acuerdo a su relación: ángulos consecutivos, ángulos complementarios, ángulos suplementarios, ángulos conjugados, ángulos opuestos por el vértice y ángulos adyacentes.
Relaciones entre ángulos Descripción: Actividad en la que podrás observar las distintas relaciones que hay entre ángulos.
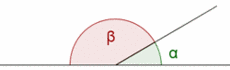
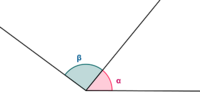
Ángulos complementarios y suplementarios (9´19") Sinopsis:Ángulos complementarios y suplementarios. Ejemplos.
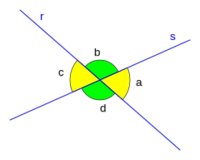
En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice.
Autoevaluación: Relaciones entre ángulos Descripción: 
