Plantilla:Determinación del dominio de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:34 12 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:36 12 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| |duracion=1'02" | |duracion=1'02" | ||
| |url1=https://www.youtube.com/watch?v=Eqdt_ED2UDk&index=4&list=PL347F4BCD040AB93F | |url1=https://www.youtube.com/watch?v=Eqdt_ED2UDk&index=4&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Estudio del dominio de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=0'48" | ||
| + | |url1=https://www.youtube.com/watch?v=TyioawvW-JA&index=5&list=PL347F4BCD040AB93F | ||
| |sinopsis=Estudio del dominio de una función a partir de su expresión analítica. | |sinopsis=Estudio del dominio de una función a partir de su expresión analítica. | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:36 12 jul 2017
El dominio de una función puede estar determinado o limitado por diferentes razones:
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
(Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, el lado no puede tomar valores negativos)
- Por voluntad de quien propone la función (Si nos interesa estudiar sólo un trozo de la función).
Ejemplos: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
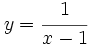
- b)
- c)
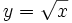
- c)
- d)
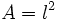 (Área de un cuadrado de lado
(Área de un cuadrado de lado 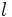 )
)
- d)
Solución:
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
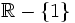 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
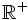 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
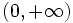 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Dominio y rango de una función. Ejemplos.
Estudio del dominio de una función a partir de su expresión analítica.
Estudio del dominio de una función a partir de su expresión analítica.
Estudio del dominio de una función a partir de su expresión analítica.
Estudio del dominio de una función a partir de su expresión analítica.
Estudio del dominio de una función a partir de su expresión analítica.

