Plantilla:Def potencia natural
De Wikipedia
| Revisión de 06:21 15 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:25 15 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| <center>[[Imagen:potenciass.gif]]{{p}}¡Ojo, no confundir!</center> | <center>[[Imagen:potenciass.gif]]{{p}}¡Ojo, no confundir!</center> | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Luisa quiere saber cuántos bisabuelos y tatarabuelos ha tenido. Para contarlos dibuja en su cuaderno su árbol genealógico: | ||
| + | |||
| + | <center>[[Imagen:familia.gif]]</center> | ||
| + | |||
| + | Ella tiene 2 padres (un padre y una madre): <math>2^1=2</math> | ||
| + | |||
| + | Cada uno de ellos tiene 2 padres. Por tanto, ella tiene <math>2 \cdot 2 = 2^2 = 4</math> abuelos. | ||
| + | |||
| + | Cada abuelo tiene a su vez 2 padres, luego ella tiene <math>2 \cdot 2 \cdot = 2^3 = 8</math> bisabuelos. | ||
| + | |||
| + | Cada bisabuelo tiene a su vez 2 padres; ella tiene <math>2 \cdot 2 \cdot 2 \cdot 2 = 2^4 = 16</math> tatarabuelos. | ||
| + | |||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{AI_descartes | {{AI_descartes | ||
| Línea 33: | Línea 47: | ||
| Haz uso de la escena anterior y contesta en tu cuaderno: | Haz uso de la escena anterior y contesta en tu cuaderno: | ||
| - | :a) ¿Qué valor tiene una las potencia cuya base es el número 0, sea cual sea el exponente? | + | # ¿Qué valor tiene una las potencia cuya base es el número 0, sea cual sea el exponente? |
| - | :b) ¿Qué valor tiene una potencia cuya base es el número 1, sea cual sea el exponente? | + | # ¿Qué valor tiene una potencia cuya base es el número 1, sea cual sea el exponente? |
| - | :c) ¿Qué valor tiene una potencia cuyo exponente es el número 1, sea cual sea la base? | + | # ¿Qué valor tiene una potencia cuyo exponente es el número 1, sea cual sea la base? |
| - | :d) Calcula <math>10^0</math>, <math>10^1</math>, <math>10^2</math>, <math>10^3</math>, <math>10^4</math>. | + | # Calcula <math>10^0</math>, <math>10^1</math>, <math>10^2</math>, <math>10^3</math>, <math>10^4</math>. |
| - | :e)Las potencias de exponente 2 se llaman '''cuadrados perfectos'''. Calcula los cuadrados de los primeros 15 números naturales. | + | # Las potencias de exponente 2 se llaman '''cuadrados perfectos'''. Calcula los cuadrados de los primeros 15 números naturales. |
| - | :f)Las potencias de exponente 3 se llaman '''cubos perfectos'''. Calcula los cubos de los primeros 15 números naturales. | + | # Las potencias de exponente 3 se llaman '''cubos perfectos'''. Calcula los cubos de los primeros 15 números naturales. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 06:25 15 jul 2017
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
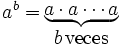 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
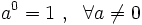 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
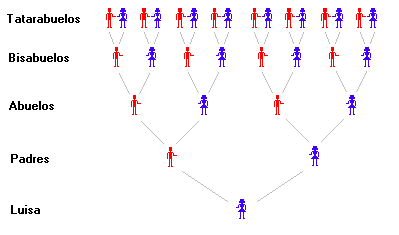
Luisa quiere saber cuántos bisabuelos y tatarabuelos ha tenido. Para contarlos dibuja en su cuaderno su árbol genealógico:
Ella tiene 2 padres (un padre y una madre): 21 = 2
Cada uno de ellos tiene 2 padres. Por tanto, ella tiene  abuelos.
abuelos.
Cada abuelo tiene a su vez 2 padres, luego ella tiene 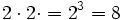 bisabuelos.
bisabuelos.
Cada bisabuelo tiene a su vez 2 padres; ella tiene 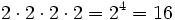 tatarabuelos.
tatarabuelos.
Observa cómo varía el resultado al modificar la base y el exponente.
Actividades:
Haz uso de la escena anterior y contesta en tu cuaderno:
- ¿Qué valor tiene una las potencia cuya base es el número 0, sea cual sea el exponente?
- ¿Qué valor tiene una potencia cuya base es el número 1, sea cual sea el exponente?
- ¿Qué valor tiene una potencia cuyo exponente es el número 1, sea cual sea la base?
- Calcula 100, 101, 102, 103, 104.
- Las potencias de exponente 2 se llaman cuadrados perfectos. Calcula los cuadrados de los primeros 15 números naturales.
- Las potencias de exponente 3 se llaman cubos perfectos. Calcula los cubos de los primeros 15 números naturales.
Definición de potencia de exponente natural. Ejemplos
Potencias de exponente cero. Ejemplos
Potencia de exponente natural. Ejemplos.
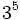 .
.
 .
.

