Probabilidad de un suceso (1º ESO)
De Wikipedia
| Revisión de 09:52 2 ago 2017 Coordinador (Discusión | contribuciones) (→La probabilidad y la ley de los grandes números) ← Ir a diferencia anterior |
Revisión de 09:53 2 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| ==Ley de los grandes números== | ==Ley de los grandes números== | ||
| {{Ley de los grandes números}} | {{Ley de los grandes números}} | ||
| - | {{p}} | ||
| - | {{Definición: Probabilidad}} | ||
| {{p}} | {{p}} | ||
| ==Probabilidad de un suceso== | ==Probabilidad de un suceso== | ||
Revisión de 09:53 2 ago 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Probabilidad (3º ESO) | WIRIS Geogebra Calculadora |
Idea intuitiva de probabilidad
- La probabilidad de un suceso aleatorio, de forma intuitiva, es el grado de confianza que podemos tener en que ese suceso ocurra.
- Para designar la probabilidad de un suceso, S, escribiremos P(S).
- La probabilidad de un suceso se expresa mediante un número comprendido entre 0 y 1:
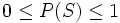
- Si P(S) es próximo a 0 diremos que el suceso S es poco probable.
- Si P(S) es próximo a 1 diremos que el suceso S es muy probable.
- Al extraer una carta de la baraja española es "poco probable" obtener el as de oros (hay una única carta entre las 40 posibles). Sin embargo es "muy probable" sacar una carta que no sea figura (hay 12 figuras y 28 que no son figuras).
- Al lanzar un dado de 6 caras es "poco probable" obtener "más de 5" (sólo existe un caso favorable de 6), y es "muy probable" sacar "más de 1" (hay 5 casos favorables de 6).
Ley de los grandes números
- Si repetimos un experimento aleatorio bajo las mismas condiciones, llamaremosfrecuencia absoluta de un suceso, al número de veces que ocurre dicho suceso.
- Llamaremosfrecuencia relativa de dicho suceso, al cociente entre la frecuencia absoluta y el número total de veces que se realiza el experimento.
- La frecuencia relativa es un número comprendido entre 0 y 1.
Frecuencia absoluta y relativa (4'39") Sinopsis:Frecuencia relativa y frecuencia absoluta. Ejemplo.
Actividad 1 Descripción: Actividades en las que podrás aprender los conceptos de frecuencia absoluta y relativa.
Actividad 2 Descripción: Actividades en las que podrás aprender los conceptos de frecuencia absoluta y relativa.
Ley de los grandes números
Un experimento aleatorio se caracteriza porque repetido muchas veces y en idénticas condiciones, su frecuencia relativa tiende a un número fijo, comprendido entre 0 y 1. Esta propiedad es conocida como ley de los grandes números, establecida por Jakob Bernouilli.
Ese número al que tiende la frecuencia es lo que llamaremos probabilidad de un suceso.
Probabilidad de un suceso
Probabilidad de un suceso es el número al que tiende la frecuencia relativa asociada al suceso a medida que aumenta el número de veces que se realiza el experimento.
Probabilidad. Ley de los grandes números Descripción: Actividades en las que podrás aprender el concepto de probabilidad y la "ley de los grandes números".
Actividad: Probabilidad. Ley de los grandes números Descripción: En esta escena veremos lo que ocurre cuando tiramos una moneda muchas veces.
- Primero tienes que elegir, en la casilla titulada "Múltiplos de", que establece de cuánto en cuánto tiramos las monedas (de 10 en 10, de 100 en 100, etc.).
- A continuación, pulsando sobre la flecha azul del control "Tiradas", simularemos el lanzamiento de monedas en la cantidad deseada.
- En cada caso obtendremos la frecuencia relativa de cada suceso, y una gráfica con el número de caras.
- Prueba con diferentes tiradas y observa el resultado de las frecuencias relativas en cada caso:
Probabilidad. Ley de los grandes números. (13'37") Sinopsis:La segunda parte de este videotutorial de 33'20" dura 5'38" y trata sobre:
- 13:35 a 19:19: La probabilidad y la ley de los grandes números. Ejemplos.
Noción de probabilidad Descripción: Actividades en las que podrás aprender el concepto de frecuencia relativa de un suceso y el de probabilidad.
