Plantilla:Parámetros de posición
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:26 3 ago 2017 Coordinador (Discusión | contribuciones) (→Diagrama de caja y bigotes) ← Ir a diferencia anterior |
Revisión de 10:27 3 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| {{AI_cidead | {{AI_cidead | ||
| |titulo1=Parámetros de posición | |titulo1=Parámetros de posición | ||
| - | |descripcion=Actividades en la que podrás aprender a calcular la mediana y los cuartiles primero y tercero de una distribución estadística. | + | |descripcion=Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística. |
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3c.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3c.htm | ||
Revisión de 10:27 3 ago 2017
Los parámetros de posición dividen un conjunto de datos en grupos con el mismo número de individuos.
Para calcular los parámetros de posición es necesario que los datos estén ordenados de menor a mayor.
Los parámetros de posición son:
- Cuartiles: Son los valores de la variable que dividen la serie de datos en cuatro partes iguales.
- Los cuartiles son tres: Q1, Q2 y Q3.
- Delimitan al 25%, al 50% y al 75% de los datos.
- Q2 coincide con la mediana.
- Deciles: Son los valores de la variable que dividen la serie de datos en diez partes iguales.
- Los deciles son 9: D1, D2 ... D9.
- Delimitan al 10%, al 20%, ..., 90% de los datos.
- D5 coincide con la mediana.
- Percentiles: Son los valores de la variable que dividen la serie de datos en cien partes iguales.
- Los deciles son 99: P1, P2 ... P99.
- Delimitan al 1%, al 2%, ..., 99% de los datos.
- P50 coincide con la mediana.
Procedimiento
Para calcular los parámetros de posición es necesario que los datos estén ordenados de menor a mayor.
- Cuartiles: Buscamos el lugar que ocupa cada cuartil mediante la expresión:
- A continuación, dependiendo de si hay un número par o impar de datos observados, procederemos como hacíamos con la mediana.
- Deciles: Buscamos el lugar que ocupa cada decil mediante la expresión:
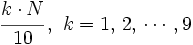
- A continuación se procede como con los cuartiles.
- Percentiles: Buscamos el lugar que ocupa cada percentil mediante la expresión:
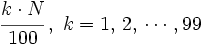
- A continuación se procede como con los cuartiles y deciles.
Parámetros de posición Descripción: Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística.
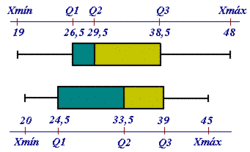
Diagrama de caja y bigotes
 Ejemplos: Diagramas de cajas y bigotes Descripción: En esta página web de "Estadística para todos" podrás encontrar ejemplos de diagramas de cajas y bigotes. Podrás aprender a construirlos y a utilizarlos para comparar distintas distribuciones. |  |
