Plantilla:Def cto num naturales
De Wikipedia
| Revisión de 17:25 6 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:19 7 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| |url1=http://www.vitutor.com/di/n/a_1e.html | |url1=http://www.vitutor.com/di/n/a_1e.html | ||
| }} | }} | ||
| + | {{Video: Numeros naturales. Numeros primos}} | ||
Revisión de 10:19 7 ago 2017
El conjunto de los números naturales es:
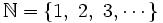
Son infinitos. Sirven para contar (números cardinales: 1, 2, 3, ...) , para ordenar (números ordinales: 1º, 2º, 3º, ...) y para identificar y diferenciar los distintos elementos de un conjunto.
Nota: Puesto que los números naturales se utilizan para contar elementos, el "cero" puede considerarse el número que corresponde a la ausencia de los mismos; dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al "cero".
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en los 100 metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
Ejercicios de autoevaluación sobre números naturales.
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)

