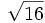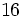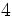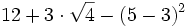Raíz cuadrada (1º ESO)
De Wikipedia
| Revisión de 07:25 8 ago 2017 Coordinador (Discusión | contribuciones) (→Operaciones combinadas) ← Ir a diferencia anterior |
Revisión de 09:09 8 ago 2017 Coordinador (Discusión | contribuciones) (→Operaciones combinadas) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| {{p}} | {{p}} | ||
| {{Jerarquia naturales}} | {{Jerarquia naturales}} | ||
| - | {{p}} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{wolfram desplegable|titulo=Operaciones combinadas|contenido= | {{wolfram desplegable|titulo=Operaciones combinadas|contenido= | ||
Revisión de 09:09 8 ago 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 34)
Raíz cuadrada de un número
La raíz cuadrada es la operación inversa de elevar al cuadrado:
La raíz cuadrada de un número  es otro número
es otro número  que elevado al cuadrado da
que elevado al cuadrado da  . Simbólicamente:
. Simbólicamente:
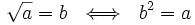
Al número  se le llama radicando y al número
se le llama radicando y al número  se le llama raíz.
se le llama raíz.
Raíz cuadrada de un número natural. Ejemplos. Obtención con la calculadora.
Raíz cuadrada de un número natural. Algoritmo para su cálculo.
Ejemplos de raíces cuadradas.
Raíces exactas y raíces enteras
Los cuadrados perfectos son los cuadrados de los números naturales:
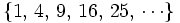
- Raíz cuadrada exacta es aquella cuyo radicando es un cuadrado perfecto.
- Raíz cuadrada inexacta es aquella cuyo radicando no es un cuadrado perfecto.
- Raíz cuadrada entera de un número es el mayor número natural cuyo cuadrado es menor o igual que dicho número. Se llama resto de la raíz cuadrada entera de un número a la diferencia entre dicho número y el cuadrado de su raíz cuadrada entera.
- La raíz cuadrada de 16 es exacta y su valor es 4, porque 16 es un cuadrado perfecto:
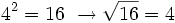
- La raíz cuadrada de 26 no es exacta y su raíz cuadrada entera es 5, porque:
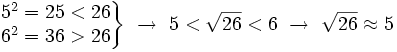
Nota: El símbolo 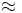 significa "aproximadamente igual".
significa "aproximadamente igual".
- Raíces cuadradas sencillas.
- Raíces cuadradas exactas y no exactas. Cálculo por exceso y por defecto.
- Ráices enteras y resto.
4 ejemplos.
Tutorial que explica el cálculo de la raíz cuadrada entera y su resto.
Halla 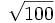 .
.
Tutorial que explica qué son los cuadrados perfectos y pone ejemplos con números menores que 100.
Tutorial que explica qué son los cuadrados perfectos y pone ejemplos con números mayores que 100.
Tutorial que explica qué son los cuadrados perfectos. La segunda parte del tutorial requiere conocer la descomposición en factores primos.
Practica con las raíces cuadradas exactas.
Practica con las raíces cuadradas enteras.
Actividad para que aprendas los cuadrados perfectos.
Raíces cuadradas de cuadrados perfectos.
Raíces cuadradas factorizando.
Raíces cuadradas exactas.
Ejercicios de autoevaluación sobre raíces cuadradas de números naturales.
Ejercicios de autoevaluación sobre raíces cuadradas exactas.
Ejercicios de autoevaluación sobre raíces cuadradas enteras.
Juego de tres en raya matemático para practicar las raíces cuadradas.
Cálculo de la raíz cuadrada por tanteo
Calcular una ráiz cuadrada por tanteo consiste en ir probando con distintos números, viendo si sus cuadrados son menores, mayores o iguales que el radicando, hasta averiguar entre qué dos cuadrados perfectos se encuentra el radicando.
Cálculo de la raíz cuadrada de un número usando el método de tanteo. Ejemplos.
Calculadora
|
Calculadora: Raíz cuadrada |
|
Actividad: Raíces cuadradas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Algoritmo de la raíz cuadrada
Cálculo de la raíz cuadrada de un número natural usando el algoritmo. Ejemplos.
Raíces de números enteros. Algoritmo.
Cómo se calculan las raíces cuadradas. Algoritmo para calcular las raíces cuadradas, paso a paso.
Ejemplos de cálculo de raíces cuadradas exactas de un número natural usando el algoritmo.
Ejemplos de cálculo de raíces cuadradas enteras de un número natural usando el algoritmo.
Calcula: 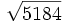
Calcula: 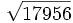
Calcula: 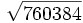
Actividades para aprender a calcular raíces cuadradas mediante el algoritmo.
En esta escena podrás practicar con el algoritmo de la raíz cuadrada.
Actividades para aprender a calcular raíces cuadradas mediante el algoritmo.
Ejercicios resueltos sobre el cálculo de raíces cuadradas usando el algoritmo.
Operaciones combinadas
Hemos introducido dos nuevas operaciones: la potencia y la raíz. Veamos como influye en la jerarquía a la hora de hacer operaciones combinadas.
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Efectúa las siguientes operaciones: 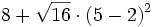
- Los paréntesis:
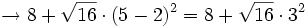
- Las potencias y las raíces:
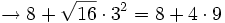
- Las multiplicaciones y divisiones:
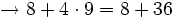
- Las sumas y restas:
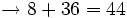
Aprende el orden en que han de hacerse las distintas operaciones con números naturales: sumas, restas, multiplicaciones, divisiones, potencias, raíces, paréntesis. Ejemplos.
Aprende el orden en que han de hacerse las distintas operaciones con números naturales.
Aprende el orden en que han de hacerse las distintas operaciones con números naturales.
¿Cuánto es 6÷2(1+2)? ¿9 ó 1?
En esta escena podrás practicar las operaciones con números naturales: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis, simples o dobles.
Ejercicios de autoevaluación sobre operaciones combinadas con números naturales.
Ejercicios propuestos
|
Ejercicios propuestos: Raíz cuadrada |
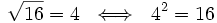
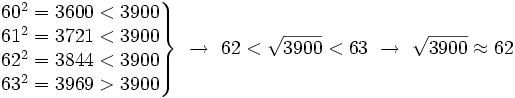 (sería la raíz entera de 3900)
(sería la raíz entera de 3900)