Plantilla:Videos ejemplos propiedades potencias racionales
De Wikipedia
| Revisión de 15:55 12 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:58 12 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| |sinopsis=<math>\left( \cfrac{a}{b} \right)^n = \cfrac{a^n}{b^n}\;</math>. Ejemplos. | |sinopsis=<math>\left( \cfrac{a}{b} \right)^n = \cfrac{a^n}{b^n}\;</math>. Ejemplos. | ||
| |url1=https://www.youtube.com/watch?v=oAcdsF4fO94&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=7 | |url1=https://www.youtube.com/watch?v=oAcdsF4fO94&list=PLo7_lpX1yruM4Eki_2jP4vJRepj5j2QS3&index=7 | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Ejemplos de potencias de fracciones | ||
| + | |duracion=10'06" | ||
| + | |sinopsis=Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=MFqwHDRFj3k&list=PLZNmE9BEzVIlaXmK5LnHeDaCapzj-V198&index=4 | ||
| }} | }} | ||
| ---- | ---- | ||
Revisión de 15:58 12 ago 2017
Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
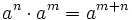 . Ejemplos.
. Ejemplos.
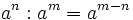 . Ejemplos.
. Ejemplos.
 . Ejemplos.
. Ejemplos.
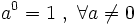 . Ejemplos.
. Ejemplos.
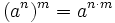 . Ejemplos.
. Ejemplos.
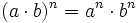 . Ejemplos.
. Ejemplos.
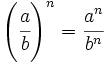 . Ejemplos.
. Ejemplos.
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica: 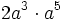
Simplifica: 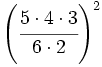
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 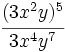
Simplifica: 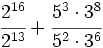
Simplifica:
- a)
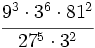
- b)
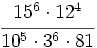
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 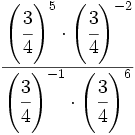
Simplifica:
- a)
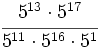
- b)
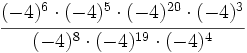
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Tutorial en el que se trabajan ejercicios de potencias en los que hay que expresar la solución como producto de potencias de base prima.
Tutorial en el que se trabajan ejercicios de potencias en los que hay que expresar la solución como una única potencia.
Cuatro ejercicios de potencias en el que se utilizan también operaciones con fracciones,productos, divisiones y potencias.

