Plantilla:Paso de fraccion a decimal
De Wikipedia
| Revisión de 08:01 7 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:03 29 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_cidead | + | {{Actividad: Paso de fracción a decimal}} |
| - | |titulo1=Paso de fracción a decimal | + | |
| - | |descripcion=#Actividad en la que podrás ver como se obtiene la expresión decimal de una fracción viendo el desarrollo de la división y los decimales que se obtienen en el cociente. | + | |
| - | #Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena. | + | |
| - | + | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_contenidos_1a.htm | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{Videos:Paso de fracción a decimal}} | {{Videos:Paso de fracción a decimal}} | ||
Revisión de 17:03 29 ago 2017
Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:- Expresión decimal exacta: Si tiene un número finito de decimales.
- Por ejemplo:
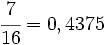 .
.
- Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.
- Por ejemplo:
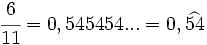 . El periodo es 54.
. El periodo es 54.
- Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.
- Por ejemplo:
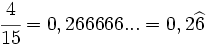 . El periodo es 6 y el anteperiodo 2.
. El periodo es 6 y el anteperiodo 2.
- Actividad en la que podrás ver como se obtiene la expresión decimal de una fracción viendo el desarrollo de la división y los decimales que se obtienen en el cociente.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
- Fracciones con expresiones decimales exactas.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
Convertir fracciones a decimales.
Cómo obtener la expresión decimal de una fracción. Ejemplos:
1. a) 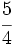 b)
b) 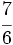
2. a) 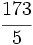 b)
b) 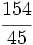 c)
c) 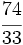
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de una fracción a su expresión decimal equivalente (finito o periódico).
Obtén la expresión decimal de 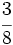
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 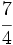
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 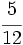
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 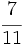
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 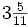
Nota: En el video, la división está realizada por el método anglosajón
Transforma en decimales las siguientes fracciones:
a) 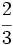 ; b)
; b) 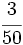 ; c)
; c) 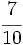 ; d)
; d) 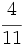 ; e)
; e) 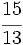
Transforma en decimales las siguientes fracciones:
a) 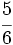 ; b)
; b) 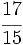 ; c)
; c) 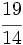 ; d)
; d) 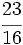
Transforma en decimales las siguientes fracciones decimales:
a) 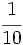 ; b)
; b) 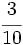 ; c)
; c) 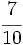 ; d)
; d) 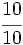 ; e)
; e) 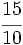 ;
;
f) 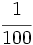 ;g)
;g) 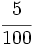 ; h)
; h) 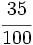 ; i)
; i) 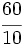 ; j)
; j) 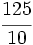 ;
;
k) 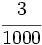 ; l)
; l) 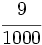 ; m)
; m) 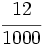 ; n)
; n) 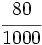 ; o)
; o) 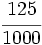 ; p)
; p)