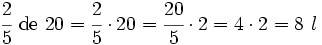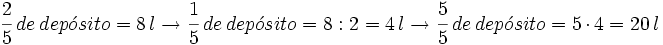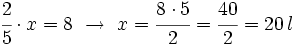Problemas con fracciones (2º ESO)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 10:24 1 sep 2017

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Calculadora

Tabla de contenidos

1 Cálculo de la fracción a partir del total y la parte
2 La fracción como operador
3 Problemas con sumas y restas de fracciones
4 Problemas con multiplicaciones y divisiones de fracciones
5 Cálculo de la fracción de otra fracción
6 Problemas
7 Ejercicios propuestos

(Pág. )

Veamos distintos casos de problemas con fracciones que nos podemos encontrar.

Cálculo de la fracción a partir del total y la parte

En este tipo de problemas nos dan dos cantidades: una que representa el total y otra que representa la parte, y se nos pide averiguar la fracción que representa la parte con respecto al total.

Procedimiento

Para calcular la fracción a partir del total y la parte, se divide la parte entre el total y se simplifica la fracción resultante.

Ejemplo: Cálculo de la fracción de una cantidad

En una empresa hay 1200 trabajadores, de los que 420 son hombres. ¿Qué fracción de mujeres y qué fracción de hombres trabajan en esta empresa?

Solución:

La fracción de hombres será:

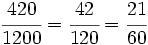
$\cfrac{420}{1200}=\cfrac{42}{120}=\cfrac{21}{60}$

En consecuencia, la de mujeres será:

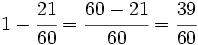
$1-\cfrac{21}{60}=\cfrac{60-21}{60}=\cfrac{39}{60}$

La fracción como operador

Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos.

Fracción de una cantidad

Para calcular una fracción a/b de una cantidad C se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por C).

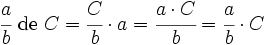
$\cfrac{a}{b} \ \mbox{de} \ C = \cfrac{C}{b} \cdot a = \cfrac{a \cdot C}{b}= \cfrac{a}{b} \cdot C$

Ejemplo 1: Cálculo de la parte conocido el total

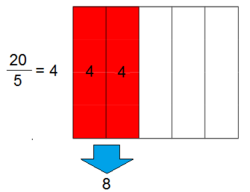
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?

Solución:

Se divide la capacidad total del depósito entre 5, que es el número de partes en que hemos dividido la unidad (el depósito). El resultado se multiplica por 2, que son las partes de depósito que estan llenas:

$\cfrac{2}{5} \ \mbox{de} \ 20=\cfrac{2}{5} \cdot 20 = \cfrac{20}{5} \cdot 2= 4 \cdot 2 = 8 \ l$

Actividades: La fracción como operador Descripción:

Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada.

Actividades: La fracción como operador Descripción:

Ejemplo 2: Cálculo del total conocida la parte

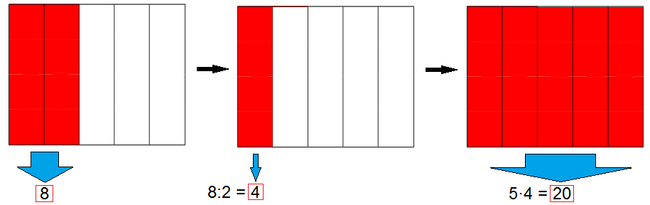
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?

Solución:

Paso a paso:

$\cfrac{2}{5} \ de \ dep \acute{o} sito = 8 \, l \rightarrow \cfrac{1}{5} \ de \ dep \acute{o} sito= 8:2=4 \, l \rightarrow \cfrac{5}{5} \ de \ dep \acute{o} sito = 5 \, \cdot \,4 = 20 \, l$

Directo:

Sea $x\;$ = capacidad del depósito.

$\cfrac{2}{5} \cdot x = 8 \ \rightarrow \ x= \cfrac{8 \cdot 5}{2} = \cfrac{40}{2}=20 \, l$

Esta técnica la aprenderemos cuando veamos las ecuaciones. De momento lo aplicaremos como una la regla práctica.

La fracción como operador

Tutorial 1 (5'14") Sinopsis:

La fracción como operador. Ejemplos.

Tutorial 2 (17'51") Sinopsis:

Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.

Tutorial 3 (1'07") Sinopsis:

Cómo se calcula la fracción de un número.

Problema 1 (3'10") Sinopsis:

He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?

Problema 2 (2'53") Sinopsis:

He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?

Problema 3 (2'32") Sinopsis:

He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?

Problemas: La fracción como operador Descripción:

Problemas sencillos con fracciones resueltos.

Autoevaluación: La fracción como operador Descripción:

Autoevaluación: Ejercicios y problemas con fracciones Descripción:

Ejercicios de autoevaluación sobre fracciones.

Problemas con sumas y restas de fracciones

Ejemplo 1: Cálculo de la parte conocido el total

Tras un fabuloso día de pesca Juan decide compartir 3 kilos de pescado con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos y a Antonio un tercio.

a) ¿Qué fracción le queda a Juan?

b)¿Cuántos kilos de pescado le queda a Juan?

Solución:

a) Como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan:

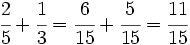
$\cfrac{2}{5}+\cfrac{1}{3}=\cfrac{6}{15}+\cfrac{5}{15}=\cfrac{11}{15}$

En consecuencia, a Juan le corresponderá:

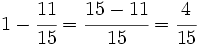
$1-\cfrac{11}{15}=\cfrac{15-11}{15}=\cfrac{4}{15}$

b) Para el segundo apartado recurriremos a lo aprendido en el primer ejemplo del apartado anterior sobre el uso dela fracción como operador, ya que tendremos que calcular los 4/15 de 3 kilos:

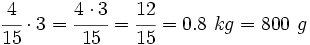
$\cfrac{4}{15} \cdot 3=\cfrac{4 \cdot 3}{15}=\cfrac{12}{15}=0.8 ~kg = 800~g$

Ejemplo 2: Cálculo del total conocida la parte

Tras un fabuloso día de pesca Juan decide compartir la pesca con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos, a Antonio un tercio y él se queda con 800 g. ¿Cuánto kilos pescó Juan?

Solución:

Al igual que en el ejemplo anterior, como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan:

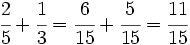
$\cfrac{2}{5}+\cfrac{1}{3}=\cfrac{6}{15}+\cfrac{5}{15}=\cfrac{11}{15}$

En consecuencia, a Juan le corresponderá:

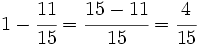
$1-\cfrac{11}{15}=\cfrac{15-11}{15}=\cfrac{4}{15}$

A continuación, para averiguar el total de la pesca, plantearemos la siguiente ecuación, igual que hacíamos en el ejemplo 2 del apartado anterior sobre el uso de la fracción como operador:

Sea $x\;$ el total de kilos que pescó Juan:

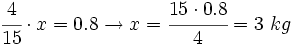
$\cfrac{4}{15} \cdot x=0.8 \rightarrow x=\cfrac{15 \cdot 0.8}{4}=3~kg$

Problemas con multiplicaciones y divisiones de fracciones

Ejemplo 1: Multiplicaciones

En una pastelería utilizan 2/5 de kilo de harina para elaborar una tarta. Si cada día hacen 25 tartas, ¿cuántos kilos de harina necesitan diariamente?

Solución:

Tendremos que multiplicar el número de tartas por la cantidad de harina que se utiliza en la elaboración de cada una:

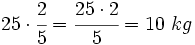
$25 \cdot \cfrac{2}{5}=\cfrac{25 \cdot 2}{5}=10~kg$

Ejemplo 2: Divisiones

En una pastelería utilizan 2/5 de kilo de harina para elaborar una tarta. Si hoy han utilizado 10 kg de harina, ¿cuántas tartas han elaborado?

Solución:

Para obtener el número de tartas que se han hecho hoy, tendremos que dividir el peso total de harina empleado entre el peso de harina que se utiliza en cada tarta:

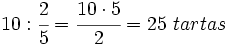
$10 : \cfrac{2}{5}=\cfrac{10 \cdot 5}{2}=25 ~tartas$

Cálculo de la fracción de otra fracción

En este tipo de problemas nos dan alguna fracción referida al total y alguna fracción referida al resto (el total menos las fracciones que nos han dado referidas al total) y se nos pide la fracción que falta para completar el total o la cantidad correspondiente a dicha fracción. También nos pueden plantear el problema de forma inversa y pedirnos la cantidad total o una de las partes.

Ejemplo 1: Cálculo de la fracción que falta

Un agricultor dedica 2/3 de su terreno a cultivar lechugas, 3/5 del resto a cultivar calabacines y el resto lo dedica a tomates. ¿Qué fracción del terreno dedica a calabacines? ¿Y a tomates?

Solución:

A lechugas dedica: 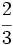$\cfrac{2}{3}$ del terreno.

El "resto" será lo que queda:

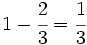$1- \cfrac{2}{3}=\cfrac{1}{3}$ del terreno

Los calabacines se calculan como la fracción de una cantidad que es otra fracción:

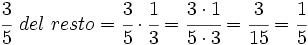
$\cfrac{3}{5}~del~resto=\cfrac{3}{5} \cdot \cfrac{1}{3}=\cfrac{3 \cdot 1}{5 \cdot 3}=\cfrac{3}{15}=\cfrac{1}{5}$

Luego dedica a calabacines: 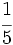$\cfrac{1}{5}$ del terreno.

Para hallar la fracción dedicada a tomates hacemos lo mismo pero con 2/5 en vez de 3/5:

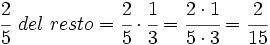
$\cfrac{2}{5}~del~resto=\cfrac{2}{5} \cdot \cfrac{1}{3}=\cfrac{2 \cdot 1}{5 \cdot 3}=\cfrac{2}{15}$

Luego dedica a tomates: 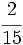$\cfrac{2}{15}$ del terreno.

Problemas

Problemas con fracciones (Nivel 1) Descripción:

Problemas con fracciones.

Problemas con fracciones (Nivel 2) Descripción:

Problemas con fracciones.

Problemas con fracciones

Problemas 1 (5'27") Sinopsis:

4 problemas:

Una caja contiene 60 galletas. Raúl se come 1/3 y Manuel 2/5. ¿Cuántas galletas se ha comido cada uno?
Pedro ha recorrido en bici 6 km, que son 3/4 de la etapa de hoy. ¿Cuál es el recorrido total de la etapa?
Alicia tiene 30€ de paga mensual. La primera semana gastó 2/5. La segunda gastó 5/6 de lo que le quedaba. ¿Cuánto gastó cada semana?.¿Cuánto le queda?
Tenemos que vaciar una piscina. Sacamos por la mañana 2/5 del agua y por la tarde 1/4 de lo que quedaba. Si la final del día había 180 litros, ¿cuál es la capacidad de la piscina?.

Problemas 2 (32'26") Sinopsis:

2 problemas:

Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 del total. ¿Cuánto trasladará el tercero?
Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 de lo que queda. ¿Cuánto trasladará el tercero?

Problemas 3 (10'18") Sinopsis:

Problemas con fracciones.

Problemas 4 (10'52") Sinopsis:

Problemas con fracciones.

Problemas 5 (16'50") Sinopsis:

Problemas con fracciones.

Problema 6 (3'36") Sinopsis:

Mi padre se ha comido 1/8 de la tableta de turrón y mi madre 2/7 de lo que quedaba. Si costó 4€, ¿cuántos céntimos se comió cada uno?.¿Qué fracción queda?

Problemas resueltos: Fracciones Descripción:

Problemas resueltos sobre fracciones.

Ejercicios propuestos

Ejercicios propuestos: Problemas con fracciones

(Pág. 77)

1, 3, 4, 5, 6, 8, 10, 11, 16, 17, 18

2, 7, 12, 13, 14, 15, 19

Obtenido de "http://maralboran.org/wikipedia/index.php/Problemas_con_fracciones_%282%C2%BA_ESO%29"

Categoría: Ejercicios de Matemáticas

 *Los '''calabacines''' se calculan como la fracción de una cantidad que es otra fracción:
-<center><math>\cfrac{3}{5}~del~resto=\cfrac{3}{5} \cdot \cfrac{1}{3}=\cfrac{3 \cdot 1}{5 \cdot 3}=\cfrac{3}{15}=\cfrac{1}{5}</math> del terreno</center>
+<center><math>\cfrac{3}{5}~del~resto=\cfrac{3}{5} \cdot \cfrac{1}{3}=\cfrac{3 \cdot 1}{5 \cdot 3}=\cfrac{3}{15}=\cfrac{1}{5}</math></center>
 {{p}}
 :Luego dedica a calabacines: <math>\cfrac{1}{5}</math> del terreno.

Problemas con fracciones (2º ESO)

De Wikipedia

Revisión de 10:24 1 sep 2017

Tabla de contenidos

Cálculo de la fracción a partir del total y la parte

La fracción como operador

Problemas con sumas y restas de fracciones

Problemas con multiplicaciones y divisiones de fracciones

Cálculo de la fracción de otra fracción

Problemas

Ejercicios propuestos

Vistas

Herramientas personales

Menú

Buscar

Herramientas