Plantilla:Videos ejemplos propiedades potencias racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:13 12 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:19 1 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 129: | Línea 129: | ||
| e) <math>6^6 \cdot 8^4 : 9^3</math> | e) <math>6^6 \cdot 8^4 : 9^3</math> | ||
| - | f) <math>\cdfrac{4^6 \cdot 9^3}{12^5}</math> | + | f) <math>\cfrac{4^6 \cdot 9^3}{12^5}</math> |
| |url1=https://www.youtube.com/watch?v=If6mSe0qgkY&list=PLZNmE9BEzVIlrsOMVfmJS3vaKVqScVudR&index=3 | |url1=https://www.youtube.com/watch?v=If6mSe0qgkY&list=PLZNmE9BEzVIlrsOMVfmJS3vaKVqScVudR&index=3 | ||
| }} | }} | ||
Revisión de 17:19 1 sep 2017
Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
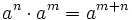 . Ejemplos.
. Ejemplos.
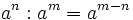 . Ejemplos.
. Ejemplos.
 . Ejemplos.
. Ejemplos.
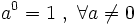 . Ejemplos.
. Ejemplos.
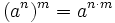 . Ejemplos.
. Ejemplos.
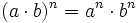 . Ejemplos.
. Ejemplos.
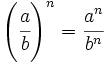 . Ejemplos.
. Ejemplos.
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica: 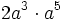
Simplifica: 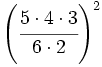
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 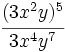
Simplifica: 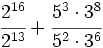
Simplifica y expresa la solución como una única potencia:
a) 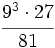
b) 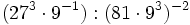
c) 
d) 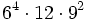
e) a) 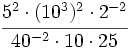
Simplifica y expresa la solución como una única potencia:
a) 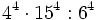
b) 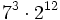
c) 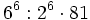
d) 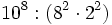
e) 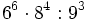
f) 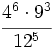
Simplifica:
- a)
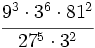
- b)
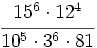
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 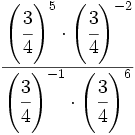
Simplifica:
- a)
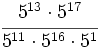
- b)
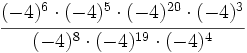
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)

