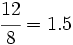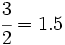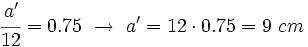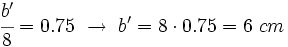Figuras semejantes (2º ESO)
De Wikipedia
| Revisión de 16:43 16 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:46 16 sep 2017 Coordinador (Discusión | contribuciones) (→Figuras semejantes) Ir a siguiente diferencia → |
||
| Línea 57: | Línea 57: | ||
| '''Solución:''' | '''Solución:''' | ||
| - | Llamemos ''a'', ''b'' y ''c'' a los lados del triángulo mayor, y ''a''', ''b''' y ''c''' a los del menor. | + | Llamemos <math>a\;</math>, <math>b\;</math> y <math>c\;</math> a los lados del triángulo mayor, y <math>a'\;</math>, <math>b'\;</math> y <math>c'\;</math> a los del menor. |
| - | Sabemos que ''a''=12, ''b''=8 y ''c''=16. | + | Sabemos que ''a''=12 cm, ''b''=8 cm y ''c''=16 cm. |
| Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75: | Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75: | ||
Revisión de 16:46 16 sep 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 194)
Figuras semejantes
- Dos figuras son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
- El tener la misma forma lo expresaremos matemáticamente diciendo que los segmentos correspondientes de una y otra figura son proporcionales, es decir, la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada razón de semejanza.
Propiedades
En dos figuras semejantes se cumple:
- Un ángulo en una de las figuras es igual al ángulo correspondiente en la otra figura.
- Una razón en una de las figuras es igual a la razón correspondiente en la otra figura.
Ejemplo 1: Figuras semejantes
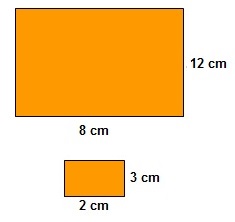
Tenemos dibujado en un papel un rectángulo de dimensiones 12 cm x 8 cm. Hacemos una fotocopia reducida y obtenemos otro rectángulo de dimensiones 3 cm x 2 cm.
- a) Comprueba que son semejantes y calcula la razón de semejanza.
- b) Calcula el procentaje de reducción aplicado en la fotocopia.
- c) Comprueba que se cumplen las propiedades de las figuras semejantes relativas a ángulos y razones.
| Solución:
a) Razón de semejanza: Si dividimos las longitudes del rectángulo pequeño entre las correspondientes del grande, obtenemos: 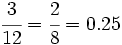 Por tanto la razón de semejanza es 0.25. b) Porcentaje: La razón de semejanza puede expresarse en porcentaje: 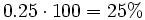 Por tanto la fotocopia es una reducción del 25%. c) Propiedades:
|
Ejemplo 2: Figuras semejantes
Dos triángulos semejantes tienen una razón de semejanza de 0.75. Si los lados del mayor miden 12, 8 y 16 cm, respectivamente, ¿cuánto miden los lados del menor?
Solución:
Llamemos  ,
,  y
y  a los lados del triángulo mayor, y
a los lados del triángulo mayor, y 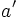 ,
,  y
y 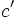 a los del menor.
a los del menor.
Sabemos que a=12 cm, b=8 cm y c=16 cm.
Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75:
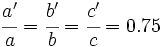
Entonces:
Ejercicios propuestos
|
Ejercicios propuestos: Figuras semejantes |