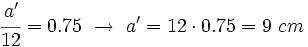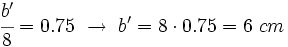Figuras semejantes (2º ESO)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 17:16 16 sep 2017
Coordinador (Discusión | contribuciones)
(→Ejercicios propuestos)
← Ir a diferencia anterior		 Revisión de 06:26 17 sep 2017
Coordinador (Discusión | contribuciones)
(→Figuras semejantes)
Ir a siguiente diferencia →
Línea 9: Línea 9:
(Pág. 194) (Pág. 194)
==Figuras semejantes== ==Figuras semejantes==
-{{Caja_Amarilla|texto=*Dos figuras son '''semejantes''' si tienen la misma forma aunque sus tamaños u orientación sean diferentes.+{{Caja_Amarilla|texto=*Dos figuras son '''semejantes''' si tienen la misma forma aunque sus tamaños u orientación sean diferentes. El tener la misma forma lo expresaremos matemáticamente diciendo que:
-*El tener la misma forma lo expresaremos matemáticamente diciendo que los segmentos correspondientes de una y otra figura son proporcionales, es decir, la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada '''razón de semejanza'''.+**Los segmentos correspondientes (u homólogos), de una y otra figura, son proporcionales.
-}}+**Sus ángulos correspondientes son iguales.
-{{p}}+*Al ser los segmentos homólogos proporcionales se cumple que la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada '''razón de semejanza'''.
-{{Teorema_sin_demo|titulo=Propiedades|enunciado=En dos figuras semejantes se cumple:+
-*Un ángulo en una de las figuras es igual al ángulo correspondiente en la otra figura.+
-*Una razón en una de las figuras es igual a la razón correspondiente en la otra figura.+
}} }}
{{p}} {{p}}
Línea 22: Línea 19:
:a) Comprueba que son semejantes y calcula la razón de semejanza. :a) Comprueba que son semejantes y calcula la razón de semejanza.
:b) Calcula el procentaje de reducción aplicado en la fotocopia. :b) Calcula el procentaje de reducción aplicado en la fotocopia.
-:c) Comprueba que se cumplen las propiedades de las figuras semejantes relativas a ángulos y razones. 
|sol= |sol=
{{Tabla50|celda2=[[Imagen:rectang_semejantes.jpg|center]]|celda1= {{Tabla50|celda2=[[Imagen:rectang_semejantes.jpg|center]]|celda1=
Línea 34: Línea 30:
Por tanto la razón de semejanza es 0.25. Por tanto la razón de semejanza es 0.25.
 +
 +Observa como los dos rectángulos tienen todos sus ángulos de 90º, es decir, la reducción no ha afectado a los ángulos.
'''b) Porcentaje:''' '''b) Porcentaje:'''
Línea 43: Línea 41:
Por tanto la fotocopia es una reducción del 25%. Por tanto la fotocopia es una reducción del 25%.
-'''c) Propiedades:''' 
- 
-*Los dos rectángulos tienen todos sus ángulos de 90º, es decir, la reducción no ha afectado a los ángulos. 
-*La razón o proporción entre sus lados tampoco se ha visto afectada por la reducción: 
-**Primer rectángulo: <math>\cfrac{12}{8} = 1.5</math>  
-**Segundo rectángulo: <math>\cfrac{3}{2} = 1.5</math>  
}} }}
}} }}
Línea 84: Línea 76:
{{p}} {{p}}
(Pág. 196) (Pág. 196)
 +
==Relación entre las áreas y los volúmenes de dos figuras semejantes== ==Relación entre las áreas y los volúmenes de dos figuras semejantes==
{{Teorema_sin_demo|titulo=Propiedades|enunciado=Si la razón de semejanza entre dos figuras es <math>k\;</math>, entonces la razón entre sus áreas es <math>k^2\;</math> y entre sus volúmenes, <math>k^3\;</math>.}} {{Teorema_sin_demo|titulo=Propiedades|enunciado=Si la razón de semejanza entre dos figuras es <math>k\;</math>, entonces la razón entre sus áreas es <math>k^2\;</math> y entre sus volúmenes, <math>k^3\;</math>.}}

Revisión de 06:26 17 sep 2017

Menú:
Enlaces internos Para repasar Para ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Calculadora

Tabla de contenidos

(Pág. 194)

Figuras semejantes

  • Dos figuras son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. El tener la misma forma lo expresaremos matemáticamente diciendo que:
    • Los segmentos correspondientes (u homólogos), de una y otra figura, son proporcionales.
    • Sus ángulos correspondientes son iguales.
  • Al ser los segmentos homólogos proporcionales se cumple que la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada razón de semejanza.

ejercicio

Ejemplo 1: Figuras semejantes

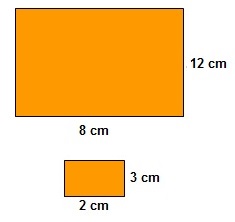
Tenemos dibujado en un papel un rectángulo de dimensiones 12 cm x 8 cm. Hacemos una fotocopia reducida y obtenemos otro rectángulo de dimensiones 3 cm x 2 cm.

a) Comprueba que son semejantes y calcula la razón de semejanza.
b) Calcula el procentaje de reducción aplicado en la fotocopia.
Solución:
Solución:

a) Razón de semejanza:

Si dividimos las longitudes del rectángulo pequeño entre las correspondientes del grande, obtenemos: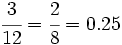

\cfrac{3}{12}=\cfrac{2}{8}=0.25

Por tanto la razón de semejanza es 0.25.

Observa como los dos rectángulos tienen todos sus ángulos de 90º, es decir, la reducción no ha afectado a los ángulos.

b) Porcentaje:

La razón de semejanza puede expresarse en porcentaje: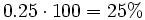

0.25 \cdot 100= 25%\;

Por tanto la fotocopia es una reducción del 25%.

ejercicio

Ejemplo 2: Figuras semejantes

Dos triángulos semejantes tienen una razón de semejanza de 0.75. Si los lados del mayor miden 12, 8 y 16 cm, respectivamente, ¿cuánto miden los lados del menor?

Solución:

Solución:

Llamemos a, b y c, a los lados del triángulo mayor, y a´, b´ y c´, a los del menor.

Sabemos que a=12 cm, b=8 cm y c=16 cm.

Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75:

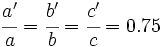
\cfrac{a'}{a}=\cfrac{b'}{b}=\cfrac{c'}{c}=0.75

Entonces:

\cfrac{a'}{12}=0.75 \ \rightarrow \ a'=12 \cdot 0.75=9~ cm
\cfrac{b'}{8}=0.75 \ \rightarrow \ b'=8 \cdot 0.75=6~ cm
\cfrac{c'}{16}=0.75 \ \rightarrow \ c'=16 \cdot 0.75=12~ cm

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Figuras semejantes

(Pág. 195)

1, 2

(Pág. 196)

Relación entre las áreas y los volúmenes de dos figuras semejantes

ejercicio

Propiedades

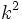Si la razón de semejanza entre dos figuras es k\;, entonces la razón entre sus áreas es k^2\; y entre sus volúmenes, k^3\;.

ejercicio

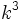Ejemplos: Relación entre las áreas y los volúmenes de dos figuras semejantes

  1. Comprueba que si un cuadrado tiene 5 cm de lado y el de otro cuadrado mide el doble, 10 cm, entonces el área de éste es el cuádruple de la del primero.
  2. Comprueba que si un cubo tiene 5 cm de arista y la de otro cubo mide el doble, 10 cm, entonces el volumen de éste es 8 veces la del primero.
Solución:

Solución 1:

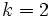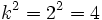En efecto, como la razón entre los lados es k=2\;, la razón entre sus áreas es k^2=2^2=4\;.

Si hallamos el área de cada cuadrado lo podremos comprobar:

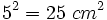
  • Área cuadrado pequeño= 5^2=25~cm^2\;
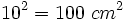
  • Área cuadrado grande= 10^2=100~cm^2\;

En efecto, el área del grande es el cuádruple del área del pequeño.

Solución 2:

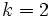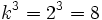En efecto, como la razón entre las aristas es k=2\;, la razón entre sus volúmenes es k^3=2^3=8\;.

Si hallamos los volúmenes de cada cubo lo podremos comprobar:

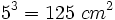
  • Volumen cubo pequeño= 5^3=125~cm^2\;
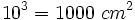
  • Volumen cubo grande= 10^3=1000~cm^2\;
En efecto, el volumen del grande es 8 veces el del pequeño.

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Relación entre las áreas y los volúmenes de dos figuras semejantes

(Pág. 196-197)

3, 4

5

Obtenido de "http://maralboran.org/wikipedia/index.php/Figuras_semejantes_%282%C2%BA_ESO%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda