Figuras semejantes (2º ESO)
De Wikipedia
| Revisión de 06:58 17 sep 2017 Coordinador (Discusión | contribuciones) (→Figuras semejantes) ← Ir a diferencia anterior |
Revisión de 06:58 17 sep 2017 Coordinador (Discusión | contribuciones) (→Figuras semejantes) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 194) | (Pág. 194) | ||
| ==Figuras semejantes== | ==Figuras semejantes== | ||
| - | {{Figuras semejantes}} | + | {{Figuras semejantes 2ºESO}} |
| {{p}} | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión de 06:58 17 sep 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 194)
Figuras semejantes
Plantilla:Figuras semejantes 2ºESO
Ejercicios propuestos
 Ejercicios propuestos: Figuras semejantes (Pág. 195)
|
(Pág. 196)
Relación entre las áreas y los volúmenes de dos figuras semejantes
Propiedades
Si la razón de semejanza entre dos figuras es 
, entonces la razón entre sus áreas es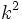 
y entre sus volúmenes, 
.
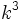Ejemplos: Relación entre las áreas y los volúmenes de dos figuras semejantes
- Comprueba que si un cuadrado tiene 5 cm de lado y el de otro cuadrado mide el doble, 10 cm, entonces el área de éste es el cuádruple de la del primero.
- Comprueba que si un cubo tiene 5 cm de arista y la de otro cubo mide el doble, 10 cm, entonces el volumen de éste es 8 veces la del primero.
Solución 1:
En efecto, como la razón entre los lados es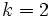 
, la razón entre sus áreas es 
.
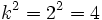Si hallamos el área de cada cuadrado lo podremos comprobar:
- Área cuadrado pequeño=
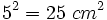
- Área cuadrado grande=
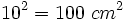
En efecto, el área del grande es el cuádruple del área del pequeño.
Solución 2:
En efecto, como la razón entre las aristas es 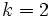, la razón entre sus volúmenes es 
.
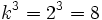Si hallamos los volúmenes de cada cubo lo podremos comprobar:
- Volumen cubo pequeño=
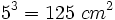
- Volumen cubo grande=
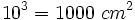
Ejercicios propuestos
Ejercicios propuestos: Relación entre las áreas y los volúmenes de dos figuras semejantes (Pág. 196-197)
|
