Plantilla:Teoremas del cateto y de la altura
De Wikipedia
| Revisión de 15:05 18 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:06 18 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 19: | Línea 19: | ||
| {{Teorema|titulo=Teorema del cateto|enunciado=En todo triángulo rectángulo, un cateto, <math>a\;</math>, es media proporcional entre la hipotenusa, <math>h\;</math>, y la proyección, <math>m\;</math> de dicho cateto sobre la hipotenusa, <math>c\;</math>. | {{Teorema|titulo=Teorema del cateto|enunciado=En todo triángulo rectángulo, un cateto, <math>a\;</math>, es media proporcional entre la hipotenusa, <math>h\;</math>, y la proyección, <math>m\;</math> de dicho cateto sobre la hipotenusa, <math>c\;</math>. | ||
| {{p}} | {{p}} | ||
| - | <center><math>\frac{a}{m}=\frac{c}{a} \ \rightarrow \ a^2=m \cdot c</math></center>|demo=Véase cualquiera de los siguientes videotutoriales. | + | <center><math>\frac{a}{m}=\frac{c}{a} \ \rightarrow \ a^2=m \cdot c</math></center> |
| Y análogamente con el otro cateto y su proyección: | Y análogamente con el otro cateto y su proyección: | ||
| <center><math>\frac{b}{n}=\frac{c}{b} \ \rightarrow \ b^2=n \cdot c</math></center>|demo=Véase cualquiera de los siguientes videotutoriales. | <center><math>\frac{b}{n}=\frac{c}{b} \ \rightarrow \ b^2=n \cdot c</math></center>|demo=Véase cualquiera de los siguientes videotutoriales. | ||
| + | |||
| + | |demo=Véase cualquiera de los siguientes videotutoriales. | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 15:06 18 sep 2017
Tutorial en el que se demuestra tanto el teorema de la altura como del cateto y aplica dichos teorema a la representación en la recta numérica de raíces cuadradas.
- 00:00 a 10:00: Demostración del Teorema de la Altura y del Cateto mediante la semejanza de triángulos.
- 10:00 a 10:35: Enunciado del Teorema de la Altura.
- 10:40 a 11:10: Enunciado del Teorema del Cateto.
- 11:10 a 15:40: Aplicación del Teorema de Pitágoras para representar raíces cuadradas..
- 15:50 a 19:45: Aplicación del Teorema de la Altura para representar raíces cuadradas..
- 19:45 a 22:15: Aplicación del Teorema del Cateto para representar raíces cuadradas.
Teorema del cateto En todo triángulo rectángulo, un cateto, 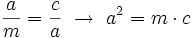 Y análogamente con el otro cateto y su proyección: 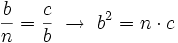 Demostración: Véase cualquiera de los siguientes videotutoriales.
Uno de los catetos de un triángulo rectángulo mide 16.5 cm y su proyección sobre la hipotenusa mide 7.5 cm. Halla el otro cateto, la proyección del otro cateto sobre la hipotenusa y la altura sobre la hipotenusa. En un triángulo rectángulo los catetos miden 20 y 21 cm. Calcula el valor de las proyecciones de los catetos sobre la hipotenusa. Teorema de la altura En todo triángulo rectángulo, la altura, 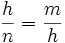 Demostración: Véase cualquiera de los siguientes videotutoriales:
Las proyecciones de los actetos sobre la hipotenusa de un triángulo rectángulo miden 18 m y 32 m, respectivamente. Halla la medida de los catetos y la de la altura sobre la hipotenusa. Problema de aplicación del teorema de la altura |
 , es media proporcional entre la hipotenusa,
, es media proporcional entre la hipotenusa, 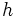 , y la proyección,
, y la proyección,  de dicho cateto sobre la hipotenusa,
de dicho cateto sobre la hipotenusa,  .
.
 .
.


