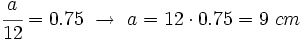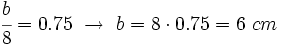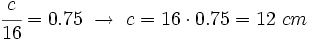Plantilla:Definición: Figuras semejantes
De Wikipedia
| Revisión de 16:57 19 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:32 22 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 97: | Línea 97: | ||
| |url1=https://www.youtube.com/watch?v=9fsk1D7Qqcw | |url1=https://www.youtube.com/watch?v=9fsk1D7Qqcw | ||
| }} | }} | ||
| - | + | {{Video_enlace_childtopia | |
| + | |titulo1=Problema 4 | ||
| + | |duracion=3'43" | ||
| + | |sinopsis=Determina si son semejantes dos rectángulos, el primero de base 3 cm y altura 6 cm, y el segundo de base 6 cm y altura 10 cm. | ||
| + | |url1=https://www.youtube.com/watch?v=8ejnXVM_vdw | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 12:32 22 sep 2017
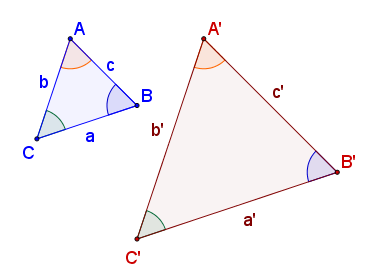
- Dos figuras son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. Esto lo expresaremos matemáticamente diciendo que:
- Los segmentos correspondientes (homólogos) son proporcionales.
- Sus ángulos correspondientes (homólogos) son iguales.
- Al ser los segmentos homólogos proporcionales, se cumple que la longitud de uno de ellos se obtiene multiplicando la longitud del correspondiente por una cantidad fija, llamada razón de semejanza.
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Ejemplos: Figuras semejantes
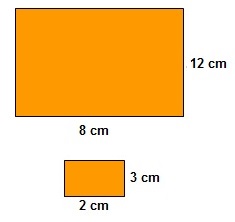
- Tenemos dibujado en un papel un rectángulo de dimensiones 12 cm x 8 cm. Hacemos una fotocopia reducida y obtenemos otro rectángulo de dimensiones 3 cm x 2 cm. Comprueba que son semejantes y calcula la razón de semejanza. Calcula el procentaje de reducción aplicado en la fotocopia.
- Dos triángulos semejantes tienen una razón de semejanza de 0.75. Si los lados del mayor miden 12, 8 y 16 cm, respectivamente, ¿cuánto miden los lados del menor?
Solución 1:
Si dividimos las longitudes del rectángulo pequeño entre las correspondientes del grande, obtenemos: 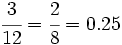 Por tanto la razón de semejanza es 0.25. Observa como los dos rectángulos tienen todos sus ángulos de 90º, es decir, la reducción no ha afectado a los ángulos.
La razón de semejanza puede expresarse en porcentaje: 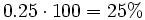 Por tanto la fotocopia es una reducción del 25%. |
| Solución 2:
Llamemos a, b y c, a los lados del triángulo menor, y a´, b´ y c´, a los del mayor. Sabemos que a´=12 cm, b´=8 cm y c´=16 cm. Como la razón de semejanza es 0.75, al dividir los lados del triángulo mayor entre sus correspondientes del menor, el resultado deberá ser 0.75: 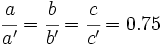 Entonces: |
Actividades para que puedas aprender los concepto de semejanza y de razón de semejanza. También podrás aprender a construir figuras semejantes a una dada.
Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
- Los ángulos correspondientes son todos iguales.
- Los segmentos correspondientes son proporcionales.
En efecto,
1. Los ángulos son iguales ya que los lados correspondientes son paralelos.
2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza.
Mueve ahora el punto rojo para comprobar el valor de r.
Dibuja un cuadrado semejante a otro de lado 2 cm, con razón de semejanza 3.
María ha dibujado dos rectángulos. El primero tiene 4 cm de base y 7 cm de altura, y el segundo tiene 12 cm de base y 21 cm de altura. ¿Son semejantes? Calcula la razón de semejanza.
Determina si son semejantes dos rectángulos, el primero de base 7 cm y altura 2 cm, y el segundo de base 14 cm y altura 4 cm. Calcula la razón de semejanza.
Determina si son semejantes dos rectángulos, el primero de base 3 cm y altura 6 cm, y el segundo de base 6 cm y altura 10 cm.