Plantilla:Poliedros regulares
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:38 20 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:42 27 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto='''Poliedro regular''' es aquel que cumple: | + | {{Caja_Amarilla|texto=*'''Poliedro regular''' es aquel que cumple: |
| # Sus caras son polígonos regulares iguales. | # Sus caras son polígonos regulares iguales. | ||
| # Todos los vértices tienen el mismo orden. | # Todos los vértices tienen el mismo orden. | ||
| + | {{p}} | ||
| + | *Sólo hay cinco poliedros regulares, los llamados '''sólidos platónicos''': | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Sólo hay cinco poliedros regulares, los llamados '''sólidos platónicos''': | ||
| <table border="0" width="100%"> | <table border="0" width="100%"> | ||
| <tr> | <tr> | ||
Revisión de 16:42 27 sep 2017
- Poliedro regular es aquel que cumple:
- Sus caras son polígonos regulares iguales.
- Todos los vértices tienen el mismo orden.
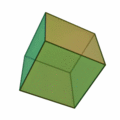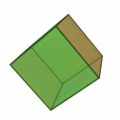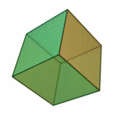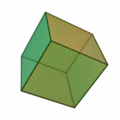
- Sólo hay cinco poliedros regulares, los llamados sólidos platónicos:
 |
 |
 |
 |
 |
Poliedros regulares (2'52") Sinopsis:Videotutorial.
El tetraedro regular (23'36") Sinopsis:El tetraedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El hexaedro regular o cubo (20'05") Sinopsis:El hexaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El octaedro regular (28'00") Sinopsis:El octaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
Ejercicio (5'03") Sinopsis:Calcula el área de un dodecaedro de 6 cm de arista y 4 cm de radio.
Poliedros regulares Descripción: En esta escena podrás ver y rotar los poliedros regulares.
Tetraedro Descripción: Actividades sobre el tetraedro.
Octaedro Descripción: Actividades sobre el octaaedro.
Hexaedro o cubo Descripción: Actividades sobre el hexaedro o cubo.
Dodecaedro Descripción: Actividades sobre el dodecaedro.
