Plantilla:Clasificación de los prismas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 06:11 28 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:13 28 sep 2017 Coordinador (Discusión | contribuciones) (→Ortoedro) Ir a siguiente diferencia → |
||
| Línea 35: | Línea 35: | ||
| {{Definición de ortoedro}} | {{Definición de ortoedro}} | ||
| {{p}} | {{p}} | ||
| - | {{AI_vitutor | ||
| - | |descripcion=Ejecicios de autoevaluación sobre los prismas. | ||
| - | |url1=https://www.vitutor.com/geo/esp/f_3e.html | ||
| - | |titulo1=Autoevaluación: ''Prismas'' | ||
| - | }} | ||
Revisión de 06:13 28 sep 2017
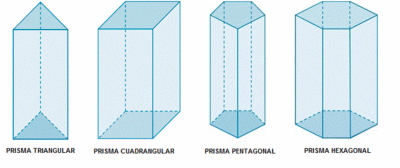
- Atendiendo a sus bases: En función del polígono de las bases, los prismas pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.
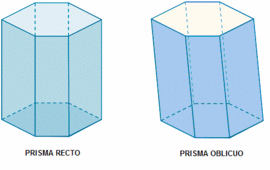
- Atendiendo a su inclinación: Si las caras laterales son perpendicualres a las bases (son rectángulos), el prisma es recto, si no , es oblicuo.
- Atendiendo a su regularidad: Un prisma es regular si su base es un polígono regular. En caso contrario es irregular. En una prisma regular, todas las aristas laterales son iguales y las caras laterales son rectángulos iguales
Clasificación de los prismas (3'11") Sinopsis:Clasificación de los prismas.
Prismas regulares Descripción: Actividad en la que se presentan distintos tipos de prismas regulares.
 Atendiendo a su inclinación
de http://calculo.cc |  Atendiendo a su base
de http://calculo.cc |
Paralelepípedos
- Los paralelepípedos son prismas en los que todas sus caras son paralelogramos.
- Las bases han de ser paralelogramos y por tanto los paralelepípedos son prismas cuadrangulares.
- Entre ellos destacamos cuatro en particular:
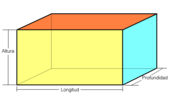
- Ortoedro: sus caras son rectángulos.
- Cubo: sus caras son cuadrados.
- Romboedro: Todas sus caras son rombos.
- Romboiedro: Todas sus caras son romboides.
Paralelepípedos Descripción: Actividad en la que podrás conocer los paralelepípedos y sus distintos tipos.
Ortoedro
|  Ortoedro
|
