Plantilla:Cálculo del máximo común divisor

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 16:09 9 nov 2017

Procedimiento artesanal

Para calcular el máximo común divisor de dos o más números se siguen los siguientes pasos:

Averiguaremos todos los divisores de dichos números.
De los divisores comunes (los que se repitan en todos) cogeremos el mayor.

Ejemplo:

Calcula el m.c.d.(24,60) por el método artesanal

Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24

Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

m.c.d.(24,60)= 12

Procedimiento artesanal Descripción:

Actividad en la que podrás ver como se obtiene el m.c.d de dos números mediante el procedimiento artesanal.

Procedimiento óptimo

Para obtener el m.c.d. de dos o más números se siguen los siguientes pasos:

Se descomponen los números en factores primos.
Se toman los factores comunes con menor exponente.
Se multiplican dichos factores y el resultado obtenido es el m.c.d.

Ejemplo:

Calcula el m.c.d.(24,60) por el método óptimo

Descomponemos 24 y 60 en sus factores primos:

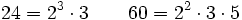
$24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5$

Multiplicando los factores comunes elevados al menor exponente:

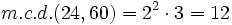
$m.c.d.(24,60)= 2^2 \cdot 3=12$

Máximo común divisor

Tutorial 1 (13´46") Sinopsis:

Tutorial que explica el significado del máximo común divisor, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los divisores de los números, para el caso de número pequeños, o el algoritmo general.

00:00 a 07:33: ¿Qué es el máximo común divisor? Método de extracción de divisores.
07:33 a 13:46: Método general para calcular el m.c.d. Ejemplos.

Tutorial 2 (9´57") Sinopsis:

Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos o tres números.

Tutorial 3 (14´36") Sinopsis:

Concepto y cálculo del máximo común divisor de dos o más números.

Tutorial 4 (3´34") Sinopsis:

Concepto de máximo común divisor. Ejemplo.

Tutorial 5 (2´04") Sinopsis:

Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos números. Desarrolla un ejemplo en el que calcula el m.c.d. mediante el método artesanal.

Ejercicio 1 (1'01") Sinopsis:

Cálcula el máximo común divisor de 12 y 20

Ejercicio 2 (6'19") Sinopsis:

Cálcula el máximo común divisor de:

a) 12 y 18

b) 360 y 84

c) 40, 72 y 300

Ejercicio 3 (5'52") Sinopsis:

Cálcula el máximo común divisor de:

a) 30 y 45

b) 36, 84 y 120

Ejercicio 4 (14'59") Sinopsis:

Cálcula el máximo común divisor de:

a) 18 y 24

b) 36, 54 y 90

Ejercicio 5 (6'22") Sinopsis:

Calcula:

a) m.c.d.(36, 48).

b) m.c.d.(60, 90, 150).

Ejercicio 6 (9´06") Sinopsis:

Calcula:

a) m.c.d.(15, 20)

b) m.c.d.(12, 18)

c) m.c.d.(16, 20, 24)

d) m.c.d.(18, 27)

Ejercicio 7 (8´10") Sinopsis:

Calcula:

a) m.c.d.(8, 20)

b) m.c.d.(96, 160, 24)

Ejercicio 8 (6'17") Sinopsis:

Calcula: m.c.d.(48, 36, 84).

Ejercicio 9 (4'46") Sinopsis:

Calcula: m.c.d.(72, 108, 60).

Ejercicio 10 (4´48") Sinopsis:

1) Calcula el m.c.d (-12, -30) hallando primero los divisores comunes.

Ejercicio 11 (6´13") Sinopsis:

2a) Calcula el m.c.d (6, -12) hallando primero los divisores comunes.

2b) Calcula el m.c.d (-12, -15) hallando primero los divisores comunes.

2c) Calcula el m.c.d (-6, 8) hallando primero los divisores comunes.

2d) Calcula el m.c.d (0, -18) hallando primero los divisores comunes.

2e) Calcula el m.c.d (6, 4) hallando primero los divisores comunes.

2f) Calcula el m.c.d (8, -72) hallando primero los divisores comunes.

Ejercicio 12 (2´09") Sinopsis:

3) Escribe los divisores de 4 y los divisores de 8.

a) ¿Es 4 divisor de 8?

b) ¿Son todos los divisores de 4 también divisores de 8?

c) ¿Es 8 divisor de 4?

d) ¿Son todos los divisores de 8 también divisores de 4?

e) ¿Cuál es el m.c.d. de 4 y 8?

Ejercicio 13 (6´15") Sinopsis:

3) Calcula hallando los divisores comunes:

a) m.c.d.(4, 16, 14)

b) m.c.d.(9, 12, 18)

c) m.c.d.(8, 16, 28)

d) m.c.d.(21, 27, 30)

Actividades: Máximo común divisor

Autoevaluación Descripción:

Ejercicios de autoevaluación sobre el m.c.d.

Juego Descripción:

Juego para practicar el m.c.d.

Autoevaluación: Máximo común divisor (Nivel avanzado) Descripción:

Ejercicios de autoevaluación sobre el m.c.d. (Nivel avanzado)

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:C%C3%A1lculo_del_m%C3%A1ximo_com%C3%BAn_divisor"

 |sinopsis=Concepto y cálculo del máximo común divisor de dos o más números.
 }}
-{{Video_enlace_mundoprimaria
+{{Video_enlace_escuela
 |titulo1=Tutorial 4
+|duracion=3´34"
+|url1=https://www.youtube.com/watch?v=2LvPEYDx5MA&index=1&list=PLw7Z_p6_h3ow7SdhMk2lKYZJE6YzZzRBN
+|sinopsis=Concepto de máximo común divisor. Ejemplo.
+}}
+{{Video_enlace_mundoprimaria
+|titulo1=Tutorial 5
 |duracion=2´04"
 |url1=https://www.youtube.com/watch?v=2-NNACxvcIk
 |url1=https://www.youtube.com/watch?v=uPzKLf0tW_Q
 }}
+{{Video_enlace_escuela
+|titulo1=Ejercicio 10
+|duracion=4´48"
+|url1=https://www.youtube.com/watch?v=uGnBdlxyVRA&index=2&list=PLw7Z_p6_h3ow7SdhMk2lKYZJE6YzZzRBN
+|sinopsis=1) Calcula el m.c.d (-12, -30) hallando primero los divisores comunes.
+}}
+{{Video_enlace_escuela
+|titulo1=Ejercicio 11
+|duracion=6´13"
+|url1=https://www.youtube.com/watch?v=Bbyu3FZW6Hs&index=3&list=PLw7Z_p6_h3ow7SdhMk2lKYZJE6YzZzRBN
+|sinopsis=
+a) Calcula el m.c.d (6, -12) hallando primero los divisores comunes.
+b) Calcula el m.c.d (-12, -15) hallando primero los divisores comunes.
+c) Calcula el m.c.d (-6, 8) hallando primero los divisores comunes.
+d) Calcula el m.c.d (0, -18) hallando primero los divisores comunes.
+e) Calcula el m.c.d (6, 4) hallando primero los divisores comunes.
+f) Calcula el m.c.d (8, -72) hallando primero los divisores comunes.
+}}
+{{Video_enlace_escuela
+|titulo1=Ejercicio 12
+|duracion=2´09"
+|url1=https://www.youtube.com/watch?v=TEWq3SFfqro&index=4&list=PLw7Z_p6_h3ow7SdhMk2lKYZJE6YzZzRBN
+|sinopsis=3) Escribe los divisores de 4 y los divisores de 8.
+:a) ¿Es 4 divisor de 8?
+:b) ¿Son todos los divisores de 4 también divisores de 8?
+:c) ¿Es 8 divisor de 4?
+:d) ¿Son todos los divisores de 8 también divisores de 4?
+:e) ¿Cuál es el m.c.d. de 4 y 8?
+}}
+{{Video_enlace_escuela
+|titulo1=Ejercicio 13
+|duracion=6´15"
+|url1=https://www.youtube.com/watch?v=kPBL4YPUWYM&list=PLw7Z_p6_h3ow7SdhMk2lKYZJE6YzZzRBN&index=5
+|sinopsis=3) Calcula hallando los divisores comunes:
+:a) m.c.d.(4, 16, 14)
+:b) m.c.d.(9, 12, 18)
+:c) m.c.d.(8, 16, 28)
+:d) m.c.d.(21, 27, 30)
+}}
 }}
 {{p}}

Plantilla:Cálculo del máximo común divisor

De Wikipedia

Revisión de 16:09 9 nov 2017

Vistas

Herramientas personales

Menú

Buscar

Herramientas