Plantilla:Definición de ecuación
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:57 10 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:03 10 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *Una '''ecuación''' es una igualdad entre expresiones algebraicas, en las que aparece una o más letras, llamadas '''incógnitas'''. Podemos tener ecuaciones con una incógnita, con dos incógnitas, etc. Las expresiones algebraicas a ambos lados de la ecuación reciben el nombre de '''miembros''' de la ecuación. | + | *Una '''ecuación''' es una igualdad entre expresiones algebraicas, en las que aparece una o más letras, llamadas '''incógnitas'''. Podemos tener ecuaciones con una incógnita, con dos incógnitas, etc. |
| + | |||
| + | *Las expresiones algebraicas a ambos lados de la ecuación reciben el nombre de '''miembros''' de la ecuación. | ||
| + | |||
| + | *Los '''términos''' de una ecuación son los monomios que forman cada uno de los miembros de la ecuación. Recuerda que los números pueden considerarse monomios de grado cero. | ||
| + | |||
| + | *El '''grado''' de una ecuación es el mayor de los grados de los monomios que aparecen en la ecuación una vez ésta ha sido reducida (simplificada). | ||
| *Una '''solución''' de una ecuación son los números (uno por cada incógnita) que hacen que la igualdad sea cierta, al sustituir las incógnitas por dichos números. | *Una '''solución''' de una ecuación son los números (uno por cada incógnita) que hacen que la igualdad sea cierta, al sustituir las incógnitas por dichos números. | ||
| Línea 32: | Línea 38: | ||
| |descripcion=Ejercicios de autoevaluación sobre ecuaciones. | |descripcion=Ejercicios de autoevaluación sobre ecuaciones. | ||
| |url1=http://www.vitutor.com/ecuaciones/1/ecua_Contenidos_e.html | |url1=http://www.vitutor.com/ecuaciones/1/ecua_Contenidos_e.html | ||
| + | }} | ||
| + | {{AI_melide | ||
| + | |titulo1=Autoevaluación: ''Ecuaciones'' | ||
| + | |descripcion=Ejercicios de autoevaluación sobre ecuaciones. | ||
| + | |url1=http://www.edu.xunta.gal/centros/iesmelide/aulavirtual2/pluginfile.php/2749/mod_imscp/content/1/significado_de_las_ecuaciones.html | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:03 10 nov 2017
En Matemáticas, cuando queremos resolver un problema, buscamos uno o varios números que cumplan las condiciones de dicho problema. Dichas condiciones suelen establecerse por medio de ecuaciones que son igualdades que relacionan las variables y números que intervienen en el problema, y que deben satisfacer los números buscados.
- Una ecuación es una igualdad entre expresiones algebraicas, en las que aparece una o más letras, llamadas incógnitas. Podemos tener ecuaciones con una incógnita, con dos incógnitas, etc.
- Las expresiones algebraicas a ambos lados de la ecuación reciben el nombre de miembros de la ecuación.
- Los términos de una ecuación son los monomios que forman cada uno de los miembros de la ecuación. Recuerda que los números pueden considerarse monomios de grado cero.
- El grado de una ecuación es el mayor de los grados de los monomios que aparecen en la ecuación una vez ésta ha sido reducida (simplificada).
- Una solución de una ecuación son los números (uno por cada incógnita) que hacen que la igualdad sea cierta, al sustituir las incógnitas por dichos números.
- Resolver una ecuación es hallar su solución o soluciones, si es que existe alguna.
- Un caso particular de ecuación es la identidad, en la que los dos lados de la igualdad son equivalentes. Por tanto, en ellas la igualdad se cumple para cualquier valor de las letras.
- Ecuaciones con una incógnita:
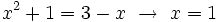es una solución.
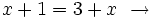No tiene solución.
- Ecuación con dos incógnitas:
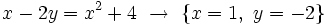es una solución.
Ecuación e identidad Descripción: Actividades en la que aprenderás a distinguir una ecuación de una identidad.
Solución de una ecuación Descripción: Actividades en la que aprenderás a comprobar si un número es solución o no de una ecuación.
Autoevaluación: Ecuaciones Descripción: Ejercicios de autoevaluación sobre ecuaciones.
Autoevaluación: Ecuaciones Descripción: Ejercicios de autoevaluación sobre ecuaciones.
