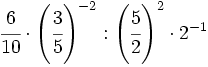Plantilla:Videos ejemplos propiedades potencias racionales
De Wikipedia
| Revisión de 09:26 11 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:15 11 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 71: | Línea 71: | ||
| }} | }} | ||
| ---- | ---- | ||
| - | {{Video_enlace_tuprofesorvirtual | + | {{Video_enlace_escuela |
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'49" | ||
| + | |sinopsis=Ejercicios 20 al 28: Producto de potencias de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=6aC_gfAZE58&index=11&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=8'36" | ||
| + | |sinopsis=Ejercicios 29 al 34: Cociente de potencias de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=PQWjTEzvjG4&index=12&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY- | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=10'26" | ||
| + | |sinopsis=Ejercicios 35 al 46: Calcular la potencia de una potencia de una fracción. | ||
| + | |url1=https://www.youtube.com/watch?v=49qBtEWXgYU&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=13 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'28" | ||
| + | |sinopsis=Ejercicios 47 al 51: Calcular potencias de productos de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=Be6PSqNjvds&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=14 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=13'54" | ||
| + | |sinopsis=Ejercicios 52 al 58: Calcular productos de potencias de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=06M-dlh6tSw&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=15 | ||
| + | }} | ||
| + | |||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=9'43" | ||
| + | |sinopsis=Simplifica: | ||
| + | :a) <math>\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3</math> | ||
| + | |||
| + | :b) <math>\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2} </math> | ||
| + | |url1=https://www.youtube.com/watch?v=KdkMb7wSV4U | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=4'05" | ||
| + | |sinopsis=Simplifica <math>\cfrac{ \left(\cfrac{3}{4} \right)^5 \cdot \left(\cfrac{3}{4} \right)^{-2}}{ \left(\cfrac{3}{4} \right)^{-1} \cdot \left(\cfrac{3}{4} \right)^6}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=mQiYuVeXZxM | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=2'08" | ||
| + | |sinopsis=Simplifica: <math>\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2 </math> | ||
| + | |url1=https://www.youtube.com/watch?v=yw1lx9htI2I | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'23" | ||
| + | |sinopsis=Ejercicios 59 al 62: Cálculos con potencias dentro de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=dhd1kiF-oPg&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=16 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=7'23" | ||
| + | |sinopsis=Ejercicios 63 al 66: Cálculos de potencias dentro de fracciones. | ||
| + | |url1=https://www.youtube.com/watch?v=Tojm9kQ1FjU&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=17 | ||
| + | }} | ||
| + | {{Video_enlace_tuprofesorvirtual | ||
| + | |titulo1=Ejercicio 3 | ||
| |duracion=3'37" | |duracion=3'37" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | ||
| Línea 78: | Línea 143: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 4 |
| |duracion=3'42" | |duracion=3'42" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | ||
| Línea 84: | Línea 149: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 5 |
| |duracion=3'40" | |duracion=3'40" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | ||
| Línea 90: | Línea 155: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 6 |
| |duracion=2'47" | |duracion=2'47" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | ||
| Línea 96: | Línea 161: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 7 |
| |duracion=17'31" | |duracion=17'31" | ||
| |sinopsis=Simplifica y expresa la solución como una única potencia: | |sinopsis=Simplifica y expresa la solución como una única potencia: | ||
| Línea 112: | Línea 177: | ||
| }} | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicio 6 | + | |titulo1=Ejercicio 8 |
| |duracion=14'41" | |duracion=14'41" | ||
| |sinopsis=Simplifica y expresa la solución como una única potencia: | |sinopsis=Simplifica y expresa la solución como una única potencia: | ||
| Línea 130: | Línea 195: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ejercicio 7 | + | |titulo1=Ejercicio 9 |
| |duracion=11'39" | |duracion=11'39" | ||
| |sinopsis=Simplifica: | |sinopsis=Simplifica: | ||
| Línea 138: | Línea 203: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 8 | + | |titulo1=Ejercicio 10 |
| |duracion=13'13" | |duracion=13'13" | ||
| |sinopsis=Simplifica: | |sinopsis=Simplifica: | ||
| Línea 148: | Línea 213: | ||
| |url1=https://www.youtube.com/watch?v=rhfNNh-alBI | |url1=https://www.youtube.com/watch?v=rhfNNh-alBI | ||
| }} | }} | ||
| - | ---- | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Ejercicios 1 | + | |titulo1=Ejercicio 11 |
| |duracion=10'06" | |duracion=10'06" | ||
| |sinopsis=Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa. | |sinopsis=Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa. | ||
| Línea 167: | Línea 231: | ||
| |url1=https://www.youtube.com/watch?v=MFqwHDRFj3k&list=PLZNmE9BEzVIlaXmK5LnHeDaCapzj-V198&index=4 | |url1=https://www.youtube.com/watch?v=MFqwHDRFj3k&list=PLZNmE9BEzVIlaXmK5LnHeDaCapzj-V198&index=4 | ||
| }} | }} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejercicio 2 | ||
| - | |duracion=9'43" | ||
| - | |sinopsis=Simplifica: | ||
| - | :a) <math>\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3</math> | ||
| - | |||
| - | :b) <math>\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2} </math> | ||
| - | |url1=https://www.youtube.com/watch?v=KdkMb7wSV4U | ||
| - | }} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 3 | ||
| - | |duracion=4'05" | ||
| - | |sinopsis=Simplifica <math>\cfrac{ \left(\cfrac{3}{4} \right)^5 \cdot \left(\cfrac{3}{4} \right)^{-2}}{ \left(\cfrac{3}{4} \right)^{-1} \cdot \left(\cfrac{3}{4} \right)^6}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=mQiYuVeXZxM | ||
| - | }} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 4 | ||
| - | |duracion=2'08" | ||
| - | |sinopsis=Simplifica: <math>\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2 </math> | ||
| - | |url1=https://www.youtube.com/watch?v=yw1lx9htI2I | ||
| - | }} | ||
| - | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:15 11 nov 2017
Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
Producto de potencias de fracciones con la misma base. Ejemplos.
Cociente de potencias de fracciones con la misma base. Ejemplos.
Potencia de otra potencia de una fracción. Ejemplos.
Potencia de un producto de fracciones. Ejemplos.
Producto de potencias de la misma base: 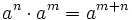 . Ejemplos.
. Ejemplos.
Cociente de potencias de la misma base: 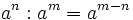 . Ejemplos.
. Ejemplos.
Potencia de otra potencia: 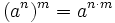 . Ejemplos.
. Ejemplos.
Potencia de un producto: 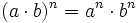 . Ejemplos.
. Ejemplos.
Potencia de un cociente: 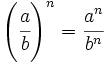 . Ejemplos.
. Ejemplos.
Ejercicios 20 al 28: Producto de potencias de fracciones.
Ejercicios 29 al 34: Cociente de potencias de fracciones.
Ejercicios 35 al 46: Calcular la potencia de una potencia de una fracción.
Ejercicios 47 al 51: Calcular potencias de productos de fracciones.
Ejercicios 52 al 58: Calcular productos de potencias de fracciones.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 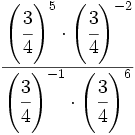
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejercicios 59 al 62: Cálculos con potencias dentro de fracciones.
Ejercicios 63 al 66: Cálculos de potencias dentro de fracciones.
Simplifica: 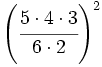
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 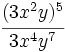
Simplifica: 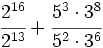
Simplifica y expresa la solución como una única potencia:
a) 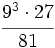
b) 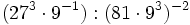
c) 
d) 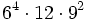
e) a) 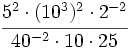
Simplifica y expresa la solución como una única potencia:
a) 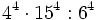
b) 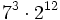
c) 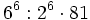
d) 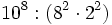
e) 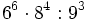
f) 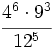
Simplifica:
- a)
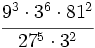
- b)
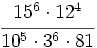
Simplifica:
- a)
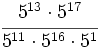
- b)
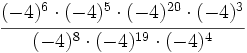
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Exponente positivo:
- a)
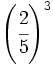 ; b)
; b)  ; c)
; c)  ; d)
; d) 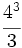 ; e)
; e) 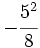
Exponente negativo:
- f)
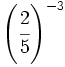 ; g)
; g) 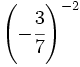 ; h)
; h) 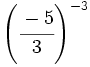 ; i)
; i) 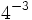 ; j)
; j) 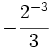
Operaciones combinadas:
- k)
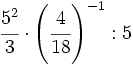 ; l)
; l)