Plantilla:Comprobación de que dos fracciones son equivalentes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:42 1 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:18 18 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Comprobación de que dos fracciones son equivalentes|enunciado=Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | + | Ya hemos visto dos maneras de comprobar que dos fracciones son equivalentes: |
| - | <center><math>\cfrac{a}{b}=\cfrac{c}{d} \quad\Leftrightarrow\quad a \cdot d=b \cdot c</math></center>}} | + | *Calculando el valor de cada una de ellas, dividiendo numerador entre denominador y viendo si el resultado es el mismo. |
| + | |||
| + | *Calculando la fracción irreducible de cada una de ellas y viendo si ambas fracciones irreducibles son iguales. | ||
| + | {{p}} | ||
| + | A continuación vamos a ver un resultado que permite hacer la comprobación de forma más simple. Lo llamaremos el método de '''multiplicar "en cruz"'''. | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Comprobación de que dos fracciones son equivalentes|enunciado= | ||
| + | Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | ||
| + | |||
| + | <center><math>\cfrac{a}{b}=\cfrac{c}{d} \quad\Leftrightarrow\quad a \cdot d=b \cdot c</math></center> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
Revisión de 18:18 18 nov 2017
Ya hemos visto dos maneras de comprobar que dos fracciones son equivalentes:
- Calculando el valor de cada una de ellas, dividiendo numerador entre denominador y viendo si el resultado es el mismo.
- Calculando la fracción irreducible de cada una de ellas y viendo si ambas fracciones irreducibles son iguales.
A continuación vamos a ver un resultado que permite hacer la comprobación de forma más simple. Lo llamaremos el método de multiplicar "en cruz".
Comprobación de que dos fracciones son equivalentes
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
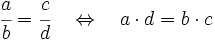
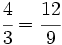 , porque
, porque 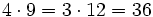 (son equivalentes)
(son equivalentes)
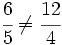 , porque
, porque 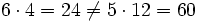 (no son equivalentes)
(no son equivalentes)

