Plantilla:La recta real
De Wikipedia
| Revisión de 19:57 23 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:00 23 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto". | La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto". | ||
| |url1=https://www.youtube.com/watch?v=GRsEFF95Zfk | |url1=https://www.youtube.com/watch?v=GRsEFF95Zfk | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Actividad: ''La recta real''|cuerpo= | ||
| + | |||
| + | |descripcion=Los números reales en la recta real. | ||
| + | {{p}} | ||
| + | Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas. | ||
| + | |||
| + | Luego introduce distintos número y observa su representación en la recta real: | ||
| + | #Introduce las fracciones <math>\cfrac{5}{3}, \cfrac{1}{7}, \cfrac{5}{4}, -\cfrac{23}{3} </math> (teclea a/b para introducir la fracción <math>\cfrac{a}{b}</math>) | ||
| + | #Introduce la raíz cuadrada de 2, 5, 7, 11 (teclea sqrt(n) para introducir la raíz cuadrada de n) | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros5_1.html | ||
| + | width=500 | ||
| + | height=200 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |url1=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros5_1.html | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 20:00 23 nov 2017
La recta real es una representación geométrica del conjunto de los números reales.
Para su construcción:
- Se elige un punto de referencia arbitrario sobre la recta al que se denomina origen y al que se le asocia el número 0.
- Se selecciona una unidad U de longitud para medir distancias que es la que separa los números 0 y 1.
- Se elige también un sentido a lo largo de la recta a la que se llama positivo y se considera como negativo al sentido opuesto.
- A cada número real p se le asocia un punto de la recta que está a una distancia de p unidades del origen en la dirección positiva o negativa, dependiendo de si el número p es positivo o negativo, respectivamente.
Los números reales. La recta real (16´23") Sinopsis: El conjunto de los números reales es la unión del conjunto de los números racionales (tienen un número finito de decimales o son periódicos) y del conjunto de los números irracionales (tienen infinitos decimales y no son periódicos). La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto".
Actividad: La recta real Descripción: Los números reales en la recta real.
Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas.
Luego introduce distintos número y observa su representación en la recta real:
- Introduce las fracciones
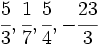(teclea a/b para introducir la fracción 
)
- Introduce la raíz cuadrada de 2, 5, 7, 11 (teclea sqrt(n) para introducir la raíz cuadrada de n)
Densidad de los números racionales e irracionales
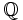es denso en 
: Entre cada dos números reales existe un racional, y por tanto hay infnitos.
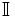es denso en : Entre cada dos números reales existe un irracional, y por tanto hay infnitos.
Completitud de los números reales
Gracias al axioma del supremo o axioma de completitud, el conjunto de los números reales cubre o completa la recta sin dejar "huecos". Existe una correspondencia biunívoca entre los puntos de la recta y los números reales de manera que a cada punto de la recta le hace corresponder un único número real y viceversa.
La recta real ampliada (8'14") Sinopsis: Este video te servirá en el tema de límites para manipular mejor expresiones con límites infinitos.
Recta real ampliada: conjunto que resulta al añadir los símbolos +∞ y -∞ al conjunto de los reales. Que quede muy claro: +∞ y -∞ no son números, y para todo real "x" es -∞ < x < +∞.
Orden en el conjunto de los reales
Dados dos números reales 
y 
, se dice que es menor que 
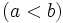, si si 
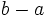es positivo. O dicho de otra forma, si está más a la derecha que en la recta real.
Actividad: Orden en el conjunto de los reales Descripción: Comparando dos números reales por su ubicación en la recta real.
Pulsa "inicio" para ver ejemplos. Fíjate que el punto rojo representa un número más pequeño que el punto azul. Mueve el punto rojo. Si los números se salen de pantalla, utiliza el zoom.
