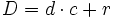Plantilla:División de naturales
De Wikipedia
| Revisión de 18:56 25 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:36 25 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 81: | Línea 81: | ||
| }} | }} | ||
| {{AI_enlace | {{AI_enlace | ||
| - | |titulo1=Ejercicio | + | |titulo1=Actividad 4 |
| |descripcion=En una división con resto 24, ¿cuál es el valor mínimo del divisor? | |descripcion=En una división con resto 24, ¿cuál es el valor mínimo del divisor? | ||
| |url1=http://scratch.mit.edu/projects/75892856/#fullscreen | |url1=http://scratch.mit.edu/projects/75892856/#fullscreen | ||
Revisión de 19:36 25 nov 2017
El siguiente video resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Videotutorial que resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
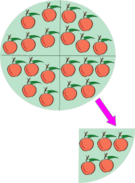
El concepto de división exacta en el conjunto de los números naturales.
División exacta y entera de números naturales. Algoritmo de la división. Ejemplos.
Repaso sobre divisiones de números naturales por 1 o 2 cifras.
Aprende a dividir por una cifra
Aprende a dividir por dos cifras
Ejercicios de divisiones por 1, 2 o 3 cifras.
En esta actividad podrás comprobar si una división dada es exacta o no.
Cálculo con divisiones.
En una división con resto 24, ¿cuál es el valor mínimo del divisor?
Ejercicios de autoevaluación sobre la división de números naturales y sus propiedades.
|
Actividad: Cociente y resto Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Ejercicio: División con naturales
Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división) |
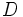 y
y 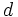 dos números naturales, con
dos números naturales, con 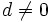 .
.
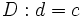
 , cociente.
, cociente.
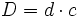 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 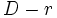 entre
entre