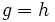Plantilla:Cilindro
De Wikipedia
| Revisión de 16:36 5 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| + | {{Caja_Amarilla|texto= | ||
| {{Tabla3 | {{Tabla3 | ||
| |celda1= | |celda1= | ||
| Línea 18: | Línea 19: | ||
| * '''Nota::'''{{p}} | * '''Nota::'''{{p}} | ||
| :<math>g=h\;\!</math> | :<math>g=h\;\!</math> | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Actividades y videos: volumen y área del cilindro}} | {{Actividades y videos: volumen y área del cilindro}} | ||
| {{p}} | {{p}} | ||
Revisión actual
En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas.
El cilindro:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen de un cilindro. Ejemplos.
Un camión cisterna tiene un depósito cilíndrico de 10 m de largo y bases de 2 m de diámetro. Calcula su capacidad en litros.
Calcula la altura de un cilindro de 825.19 cm3 de volumen y 6 cm de radio de la base.
En un depósito de gasolina de forma cilíndrica con una base de 3 m de diámetro y una profundidad de 12 m. Calcula el área total.
El área de la base de un cilindro es 25π cm2 y la generatriz es el doble del radio. Halla el volumen.
Si quieres cubrir un cilindro con tela, calcula el área de tela necesaria teniendo en cuenta que el cilindro mide 6 m de altura y 2 m de radio de la base.
Dos cilindros tienen la misma superficie lateral y sus radios miden 6 m y 8 m, respectivamente. Calcula sus alturas sabiendo que se diferencian en 3 m. Halla también sus superficies laterales.
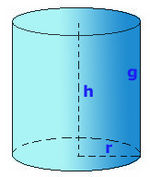
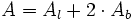
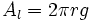
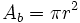
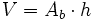
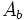 : Área de la base.
: Área de la base.
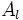 : Área lateral.
: Área lateral.
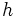 : altura.
: altura.
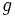 : generatriz.
: generatriz.
 : radio.
: radio.