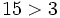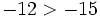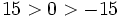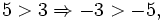Plantilla:Relación de orden
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:49 12 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:12 12 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado= | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| *Todo número negativo es menor que cero y todo número positivo es mayor que cero. | *Todo número negativo es menor que cero y todo número positivo es mayor que cero. | ||
| - | *Si dos enteros son positivos, el mayor es el que tiene mayor valor absoluto. | + | *Si dos números son positivos, el mayor es el que tiene mayor valor absoluto. |
| - | *Si dos enteros son negativos, el mayor es el que tiene menor valor absoluto. | + | *Si dos números son negativos, el mayor es el que tiene menor valor absoluto. |
| *Si a > b, entonces -b > -a | *Si a > b, entonces -b > -a | ||
| }} | }} | ||
Revisión de 08:12 12 dic 2017
Un número es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Relación de orden
Dados dos números cualesquiera, 
y 
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
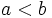(Se lee "a es menor que b").
- El primero es igual que el segundo:
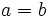(Se lee "a es igual que b").
- El primero es mayor que el segundo:
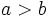(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
)
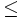- Mayor o igual que (
)
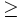- Distinto (
)
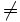Propiedades
- Todo número negativo es menor que cero y todo número positivo es mayor que cero.
- Si dos números son positivos, el mayor es el que tiene mayor valor absoluto.
- Si dos números son negativos, el mayor es el que tiene menor valor absoluto.
- Si a > b, entonces -b > -a
