Plantilla:Ecuaciones equivalentes 1ºESO
De Wikipedia
| Revisión de 10:16 12 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 39: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ecuaciones equivalentes|enunciado= | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial 1a | ||
| - | |duracion=2'33" | ||
| - | |sinopsis=1ª parte de un tutorial que consta de 5 partes: | ||
| - | |||
| - | Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=yQVgQsBvTDA | ||
| - | }} | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial 1b | ||
| - | |duracion=3'25" | ||
| - | |sinopsis=2ª parte de un tutorial que consta de 5 partes: | ||
| - | |||
| - | Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=ny7MeAmeFm8 | ||
| - | }} | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial 1c | ||
| - | |duracion=3'15" | ||
| - | |sinopsis=3ª parte de un tutorial que consta de 5 partes: | ||
| - | |||
| - | Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=UCJ8dB_JKms | ||
| - | }} | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial 1d | ||
| - | |duracion=4'40" | ||
| - | |sinopsis=4ª parte de un tutorial que consta de 5 partes: | ||
| - | |||
| - | Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=xTl_Z9-i1H4 | ||
| - | }} | ||
| - | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial 1e | ||
| - | |duracion=3'15" | ||
| - | |sinopsis=5ª parte de un tutorial que consta de 5 partes: | ||
| - | |||
| - | Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas o la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=LAxRd5XQIBs | ||
| - | }} | ||
| - | |||
| {{Video_enlace_angelmartinez | {{Video_enlace_angelmartinez | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=ecuaciones equivalentes |
| |duracion=1'00" | |duracion=1'00" | ||
| |sinopsis=Ecuaciones equivalentes. Técnicas para obtener ecuaciones equivalentes. | |sinopsis=Ecuaciones equivalentes. Técnicas para obtener ecuaciones equivalentes. | ||
| |url1=https://www.youtube.com/watch?v=xLnMPiZaXt0 | |url1=https://www.youtube.com/watch?v=xLnMPiZaXt0 | ||
| - | }} | ||
| }} | }} | ||
| {{Actividades|titulo=Ecuaciones equivalentes|enunciado= | {{Actividades|titulo=Ecuaciones equivalentes|enunciado= | ||
Revisión actual
Dos ecuaciones son equivalentes si tienen las mismas soluciones.
Ejemplo 1:
La ecuación
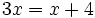 [1]
[1]es equivalente a
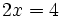 [2]
[2]Esto es así porque si en la ecuación [1] restas  a ambos miembros, la igualdad se mantiene porque hemos quitado la misma cantidad a dos expresiones que eran iguales. Así tenemos que
a ambos miembros, la igualdad se mantiene porque hemos quitado la misma cantidad a dos expresiones que eran iguales. Así tenemos que
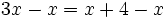
Agrupando las incógnitas en ambos miembros se obtiene
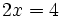
que es la ecuación [2]. Por tanto [1] y [2] son equivalentes. De hecho se puede comprobar fácilmente que ambas tienen como solución  .
.
Ejemplo 2:
La ecuación
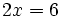 [1]
[1]es equivalente a
 [2]
[2]Esto es así porque si en la ecuación [1] divides por 2 ambos miembros, la igualdad se mantiene porque hemos dividido por la misma cantidad dos expresiones que eran iguales. Así tenemos que
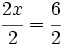
y simplificando se obtiene la ecuación [2]. Fíjate que ambas ecuaciones tienen como solución x=3.
Ecuaciones equivalentes. Técnicas para obtener ecuaciones equivalentes.
Actividades en la que aprenderás lo que son ecuaciones equivalentes y cómo se obtienen.
Actividades en la que aprenderás lo que son ecuaciones equivalentes y cómo se obtienen.

