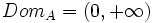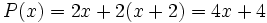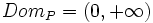Plantilla:Expresión analítica de una función
De Wikipedia
| Revisión de 19:17 11 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:45 25 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 68: | Línea 68: | ||
| |url1=https://www.youtube.com/watch?v=25VPnBQD3LA | |url1=https://www.youtube.com/watch?v=25VPnBQD3LA | ||
| }} | }} | ||
| - | {{Video_enlace_abel | + | {{Video_enlace_khan |
| |titulo1=Ejercicio 3 | |titulo1=Ejercicio 3 | ||
| - | |duracion=14'17" | + | |duracion=2'50" |
| - | |sinopsis=Representa gráficamente la función <math>y=2x+1\;</math>. | + | |sinopsis=Dada la ecuación ''4a + 7b = -52'', encuentra la expresión analítica de la función ''a = f(b)'' que relacione la variable independiente ''b'' con la variable dependiente ''a'', es decir, que exprese ''a'' en función de ''b''. |
| - | |url1=https://www.youtube.com/watch?v=K-C6l6tH95Q | + | |url1=https://youtu.be/Ug-g022lSGk |
| }} | }} | ||
| ---- | ---- | ||
Revisión de 12:45 25 dic 2017
La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.
Ejemplo: Expresión analítica de una función
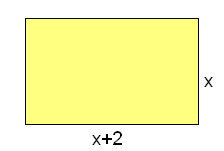
Un rectángulo mide 2 cm más de largo que de ancho.
- Halla la expresión analítica de la función que relaciona su área con su lado menor. Halla su dominio.
- Halla la expresión analítica de la función que relaciona su perímetro con su lado menor. Halla su dominio.
- Haz una tabla de valores para cada función.
- Representa gráficamente las dos funciones anteriores.
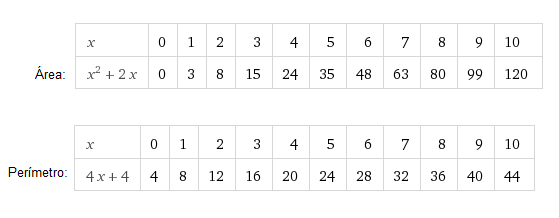
3. Tablas de valores:
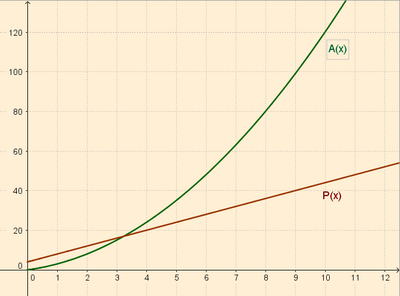
4. Representación gráfica: A partir de los valores de las tablas anteriores, dibujamos los puntos de las gráficas: la dell área (en verde) y la del perímetro (en marrón).
Actividades con las que aprenderás a obtener la expresión analítica de una función descrita mediante un enunciado.
Tutorial en el que se explican los conceptos básicos de la función y de su expresión analítica (expresión en forma de fórmula): variable independiente, dependiente, imagen, preimagen, dominio, recorrido...
Representación gráfica de funciones básicas
Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba. Obtén la expresión analítica que relaciona el volumen "V" de la caja en función del lado "x".
Expresa el área "A" de un triángulo equilátero en función de sus lado "L".
Dada la ecuación 4a + 7b = -52, encuentra la expresión analítica de la función a = f(b) que relacione la variable independiente b con la variable dependiente a, es decir, que exprese a en función de b.
Tutorial en el que se trabaja con las funciones definidas por partes en fórmulas, cálculo de imágenes y preimágenes de valores.
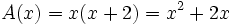
 , no puede ser un número negativo, su dominio es:
, no puede ser un número negativo, su dominio es: