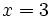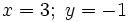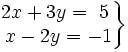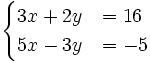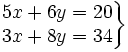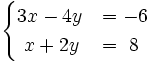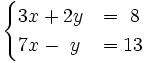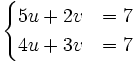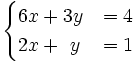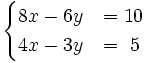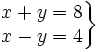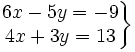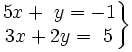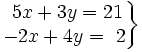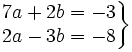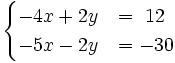Plantilla:Método de reducción
De Wikipedia
| Revisión de 00:09 28 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:48 28 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 151: | Línea 151: | ||
| |url1=https://www.youtube.com/watch?v=tg8gfUBICdQ&list=PLo7_lpX1yruOtry1_Zpf4jZg738fjkB5n&index=5 | |url1=https://www.youtube.com/watch?v=tg8gfUBICdQ&list=PLo7_lpX1yruOtry1_Zpf4jZg738fjkB5n&index=5 | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 12 | ||
| + | |duracion=6´23" | ||
| + | |url1=https://youtu.be/hCCQkExviHQ | ||
| + | |sinopsis=Resuelve por el método de reducción: | ||
| + | |||
| + | :<math>\begin{cases}-4x+2y & = ~12 \\ -5x-2y & = -30 \end{cases}</math> | ||
| }} | }} | ||
| }} | }} | ||
| Línea 160: | Línea 168: | ||
| }} | }} | ||
| {{AI_vitutor | {{AI_vitutor | ||
| - | |titulo1=Autoevaluación | + | |titulo1=Autoevaluación 1 |
| + | |descripcion=Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/equivalent-systems-of-equations/e/systems_of_equations_with_elimination_0.5 | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación 2 | ||
| |descripcion=Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales. | |descripcion=Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales. | ||
| |url1=http://www.vitutor.com/ecuaciones/sistemas/reso_2_e.html | |url1=http://www.vitutor.com/ecuaciones/sistemas/reso_2_e.html | ||
Revisión de 07:48 28 dic 2017
Procedimiento
Para resolver un sistema por el método de reducción se siguen los siguientes pasos:
- Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados, de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones.
- Se suman las ecuaciones del nuevo sistema, desapareciendo así la incógnita con coeficientes opuestos.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de reducción
Resuelve por el método de reducción el siguiente sistema:
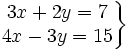
- Multiplicamos la primera ecuación por 4 y la segunda por (-3)
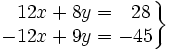
- Sumamos miembro a miembro las dos ecuaciones:
|
|
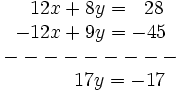
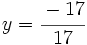
- Sustituimos el valor
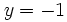en cualquiera de las dos ecuaciones del sistema de partida, por ejemplo en la primera: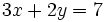 
|
|
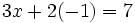
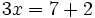
- Así, la solución del sistema es:
|
|
Tutorial 1 (0'50") Sinopsis: Método de reducción. Ejemplo.
Tutorial 2 (9'10") Sinopsis:Resolución de sistemas por reducción. Ejemplos.
Tutorial 3 (15'40") Sinopsis:Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método de reducción.
Ejercicio 1 (5'25") Sinopsis: Resuelve por el método de reducción:
Ejercicio 2 (7'40") Sinopsis:Resuelve por el método de reducción:
Ejercicio 3 (5'42") Sinopsis: Resuelve por el método de reducción:
Ejercicio 4 (4´14") Sinopsis: Resuelve por el método de reducción:
Ejercicio 5 (10´54") Sinopsis: Resolución de sistemas lineales 2x2 por el método de reducción:
Ejercicio 6 (7´18") Sinopsis: Resolución de sistemas lineales 2x2 por el método de reducción:
Ejercicio 7 (3'43") Sinopsis: Resuelve gráficamente:
Ejercicio 8 (6'15") Sinopsis: Resuelve gráficamente:
Ejercicio 9 (6'01") Sinopsis: Resuelve gráficamente:
Ejercicio 10 (5'30") Sinopsis: Resuelve gráficamente:
Ejercicio 11 (6'00") Sinopsis: Resuelve gráficamente:
Ejercicio 12 (6´23") Sinopsis: Resuelve por el método de reducción:
Actividad Descripción: Actividades en las que aprenderás el método de reducción para resolver sistemas de ecuaciones lineales con dos incógnitas.
Autoevaluación 1 Descripción: Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos Descripción: Ejercicios resueltos sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
